编程基础之机器数和算术溢出
一文深入理解计算机底层数据存储的形式,以及数据存储中的机器数(原码,反码,补码)和算术溢出等概念。
更多相关编程基础内容,请关注博主 Hexo 博文系列:
预备知识
我们知道,由于计算机的硬件决定,任何存储于计算机中的数据,计算机底层存储数据时都使用的是二进制形式。详情请参考 >>>> 【计算机中信息的存储】。
并且,
[1] >>>> 计算机只有加法运算器
根据冯·诺依曼提出的经典计算机体系结构框架,一台计算机由运算器、控制器、存储器、输入和输出设备组成。
目前,计算机中运算器只有加法运算器,没有减法运算器(据说一开始是有的,后来由于减法运算器硬件开销太大,被废了)。那如何进行减法运算???
我们知道,减去一个数可以看作加上这个数的相反数,计算机中没办法直接做减法的,但是可以通过加法运算来实现减法功能。
有个前提 >>>> 必须要有负数的概念,这就得向二进制数中引入符号位了。
| ================================================== Split Line =============================================== |
[2] >>>> 机器数 && 真值
机器数 >>> 一个数在计算机的存储形式是二进制数,我们称这些二进制数为机器数。机器数是有符号,在计算机中用机器数的最高位存放符号位,0 表示正数,1 表示负数。
由于存在符号位,以机器数 1000 0111 为例,机器数的形式值(135,无符号数)不等于其真正的值(-7,有符号数)。
机器数的真值 >>> 将带符号的机器数的真正表示的值称为机器数的真值(有符号数值)。
| ================================================== Split Line =============================================== |
[3] >>>> 内存存储的是二进制补码
计算机在存储一个数字时,并不是直接存储该数字对应的二进制数字(原码),而是存储该数字对应二进制数字的补码。
原码、反码、补码的产生过程就是为了解决计算机做减法和引入符号位的问题(后续会告诉你为什么)。
原码 && 反码 && 补码
这一小节来看原码、反码和补码到底是个啥?
为了方便说明问题,这里我们假定用 4 位二进制数表示一个整数。
原码
原码的表示与机器数真值表示的一样,即用第一位表示符号,其余位表示数值。
例如,十进制的的正负 1,用 4 位二进制的原码表示如下:
【+1】= 原:[ 0001 ]
【-1】= 原:[ 1001 ]
所有机器数的原码表示如下:
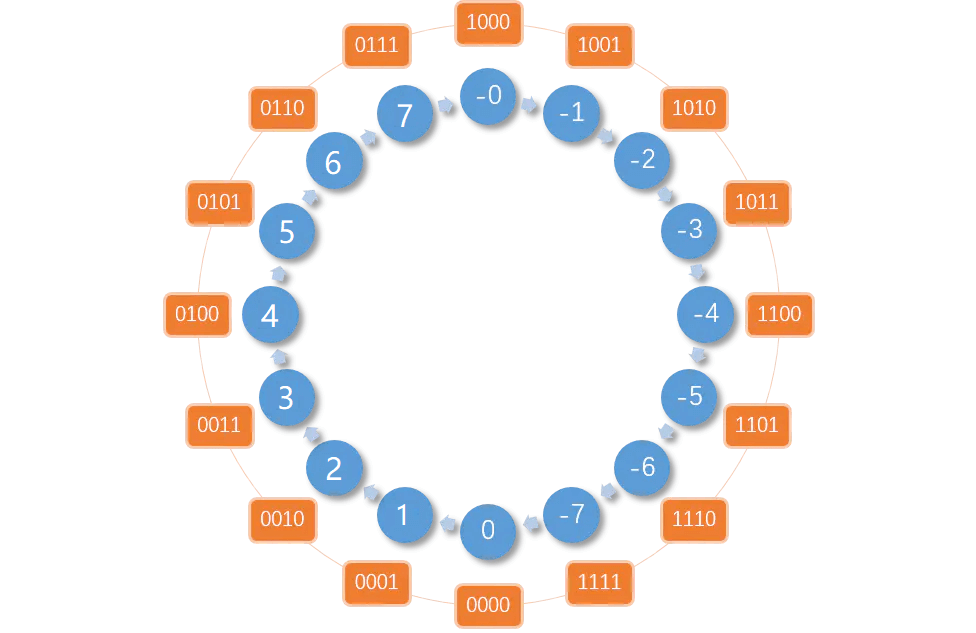
可以看到,使用原码来表示一个有符号数会带来两个问题:
- 第一个问题 >>> 正负相加不等于零:
1 + (−1)–>0001 + 1001=1010,按照原码表示等于−2; - 第二个问题 >>> 同时存在两个零,分别为
0000和1000。
可见,原码不适合用来表示有符号数!!!
为了保证正负相加等于零,引入了反码:
反码
反码的表示方法为:
- 正数的反码是其原码本身;
- 负数的反码是在其原码的基础上,符号位不变,其余按位取反。
【+1】= 原: [ 0001 ] = 反:[ 0001 ]
【-1】 = 原:[ 1001 ] = 反:[ 1110 ]
对照上面原码表(看成一个钟表),你可以将机器数 1000 想象成钟表中的 12 点,把机器数 0000 想象成钟表中 6 点,我们知道正数的反码是其本身,这也就意味着左边表盘不变动。那么,如何变动右表盘可以使得正负相加等于零???
采用反码的表示方法,负数 >>> 原码就是从 12 点开始 【顺时针】 排列 -1 到 -7,其反码是从 6 点开始 【逆时针】 排列 -1 到 -7。反码表如下:
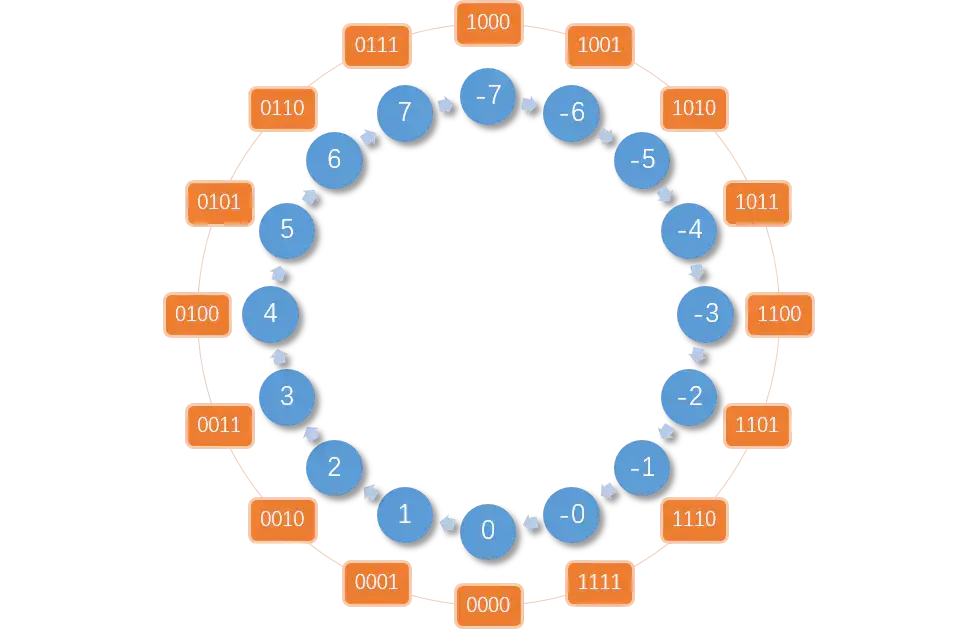
可以看到,第一个问题解决了(正负相加等于零),但是第二个问题还是没有解决,依然存在两个零,分别为 0000 和 1111。
补码就是为了解决这个问题而发明的….
聪明如你肯定想到,好解决啊~让负数反码整体顺时针移动一位,把 -0 “顶掉” 就可以了,这样对于位置 1000 还空出来一个,还可以用来多存放一个数值。
补码
事实上, 你可以如此理解~~~
补码的表示方法为:
- 正数的补码是其原码本身;
- 负数的补码是在其原码的基础上,符号位不变,其余按位取反后加
1(即在反码的基础上加1)。
【+1】= 原: [ 0001 ] = 反:[ 0001 ] = 补:[ 0001 ]
【-1】 = 原:[ 1001 ] = 反:[ 1110 ] = 补:[ 1111 ]
对于位置 1000 空出的位置还可以用来表示 -8,直接给出补码表:
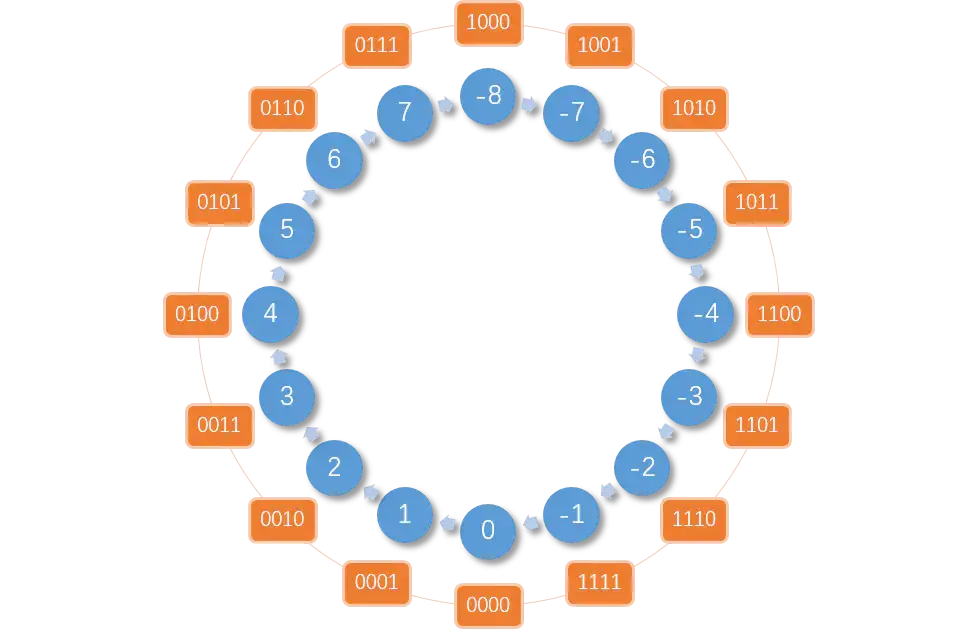
注意 >>> 实际上,还使用以前的 -0 的补码来表示 8,所以 8 并没有原码和反码表示,只要补码是 [1000],其十进制数值就为 8。
在验证以下第一个问题:如果丢弃最高位的进位,结果满足正负相加等于零。Niu 啊~~~
牢记 4 位机器数的补码表规律,并将其推到更一般的 8 位机器数 >>>
8 位机器数原码、反码可表示范围:[-127, -1],[10000000(-0)],[0, 127],共 2^8 = 256 种组合。
8 位机器数补码可表示范围:[-128, -1],[0, 127],注意 [100000000(-128)] 没有原码和反码表示。这也可以解释为什么计算机中一个字节的取值范围是 [-128,127]。
已知补码如何求原码 >>>>
当补码最高位为 0 时,即该数是正数,正数的原码、反码、补码都是一样的。
当补码最高位为 1 时,该数为负数,再对补码求补码即为原码。
算术溢出
这里我们来讨论一个在实际编写程序中非常危险的一个bug,例如 C 语言种的整型数溢出问题。
我们知道,有符号数在计算机内部都是通过补码来表示的。
上述补码表中可以看出,如果数值加上 x,就代表着顺时针走 x 格;如果数值减去 x,就代表着逆时针走 x 格。
如果 3 + 1,那就是从 3 顺时针走一格,等于 4,这是没有任何问题。但是如果是 7 + 1 呢?顺时针走 1 格后,变成了 −8 了。如果 7 + 7 呢,顺时针走 7 格,等于 −2 了。这就是整型数发生了溢出。
所谓的溢出,就是因为 4 位二进制数,用补码表示一个整数的时候,所能表示的最大正整数就是 2^(4-1)-1=7,如果在 7 的基础上再加 1,就会发生 “轻微溢出”,变为了最小的那个负数;如果两个最大的正整数相加,就会发生“严重溢出”。同理,最小的负数 -8 逆时针走 1 位,以及走 8 位对应如上。
所谓的 “轻微溢出” 和 “严重溢出” 都是从溢出的角度去定义的。事实上,它们都是非常严重的 bug,在实际编程中并不是说 “严重溢出” 就比 “轻微溢出” 更严重。
=======================
参考链接:https://www.jianshu.com/p/ffc97c4d2306
install_url to use ShareThis. Please set it in _config.yml.Like this article? Support the author with
Comments
shortname for Disqus. Please set it in _config.yml.