编程基础之进制详解
计算机组成原理中的二进制、八进制、十进制、十六进制以及进制转换。
更多相关编程基础内容,请关注博主 Hexo 博文系列:
什么是进制?
在生活中,我们通常都是使用阿拉伯数字计数的,也就是 10 进制,以 10 为单位,逢十进一(满十进一),借一当十,也因为只有 0,1,2、3、4、5、6、7、8、9 十个数字组成的,所以叫做十进制(Decimal)。十进制是在人类社会发展过程中自然形成的,它符合人们的思维习惯,例如人类有十根手指,也有十根脚趾。
那么什么是进制呢?进制也就是 进位制 >>>>
对于任何一种进制(X 进制),进行加法运算时都表示某一位置上的数运算时是逢 X 进一位,进行减法运算时都表示某一位置上的数运算时借一当 X,这就是 X 进制。这种进位制,包含 X 个数字(0 ~ X-1),基数为 X。
例如:十进制有 0~9 共 10 个数字,基数为 10,在加减法运算中,逢十进一,借一当十;二进制就是逢二进一(借一当二,0~1),八进制就是逢八进一(借一当八,0~7), 十六进制是逢十六进一(借一当十六,0~F),以此类推……
常用进制
计算机常用进制有:二进制、八进制、十六进制。
二进制
二进制(Binary)有 0~1 共 2 个数字,基数为 2,在加减法运算中,逢二进一,借一当二。
例如,数字 0、1、10、111、100、1000001` 都是有效的二进制。
了解计算机组成原理的看客老爷应该知道,在计算机内部,数据都是以二进制的形式存储的,计算机硬件无法识别除了 0/1 以外的任何数(参见:[>>> 编程基础之机器数和算术溢出 <<<]),所以二进制是学习编程必须掌握的基础。
二进制加减法 >>>>
二进制加减法和十进制加减法的思想是类似的:
- 对于十进制,进行加法运算时逢十进一,进行减法运算时借一当十;
- 对于二进制,进行加法运算时逢二进一,进行减法运算时借一当二。
下面来演示二进制加减法运算的全过程:
[1] –> 二进制加法:1+0=1、1+1=10、11+10=101、111+111=1110
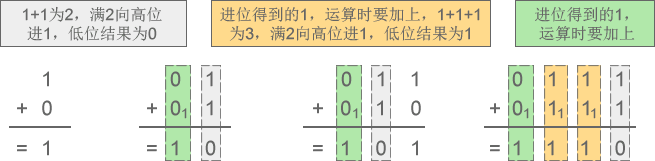
[2] –> 二进制减法:1-0=1、10-1=1、101-11=10、1100-111=101

八进制
除了二进制,计算机程序设计语言中还会使用到八进制。
八进制(Octonary)有 0~7 共 8 个数字,基数为 8,在加减法运算中,逢八进一,借一当八。
数字 0、1、5、7、14、733、67001、25430 都是有效的八进制。
下面来演示八进制加减法运算的全过程:
[1] –> 八进制加法:3+4=7、5+6=13、75+42=137、2427+567=3216
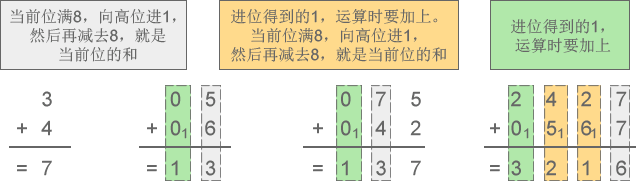
[2] –> 八进制减法:6-4=2、52-27=23、307-141=146、7430-1451=5757
十六进制
除了二进制和八进制,计算机程序设计语言中十六进制也经常使用,甚至比八进制还要频繁。
十六进制(Hexadecimal)中,用 A 来表示 10,B 表示 11,C 表示 12,D 表示 13,E 表示 14,F 表示 15,因此有 0~F 共 16 个数字,基数为 16,在加减法运算中,逢十六进一,借一当十六。
注意,十六进制中的字母不区分大小写,
ABCDEF也可以写作abcdef。
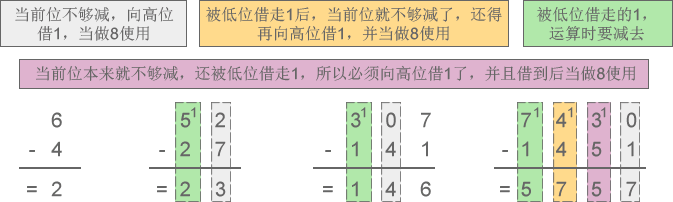
下面来演示十六进制加减法运算的全过程:
[1] –> 十六进制加法:6+7=D、18+BA=D2、595+792=D27、2F87+F8A=3F11
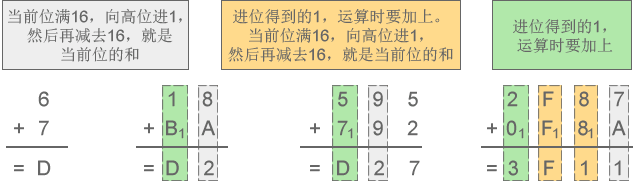
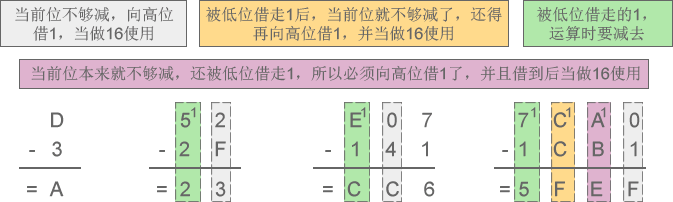
[2] –> 十六进制减法:D-3=A、52-2F=23、E07-141=CC6、7CA0-1CB1=5FEF
进制转换
上节我们对二进制、八进制和十六进制进行了说明,这里讲解不同进制之间的转换,这在编程中经常会用到:
将二进制、八进制、十六进制转换为十进制
二进制、八进制和十六进制向十进制转换都非常容易,就是 “按权相加”。所谓 “权”,也即“位权(权重)”。
假设当前数字是 N 进制,那么:
- 对于整数部分,从右往左看,第 i 位的权重等于 Ni-1;
- 对于小数部分,从左往右看,第 i 位的权重为 N-i(
0包含在整数部分)。
更加通俗的理解是,假设一个多位数(由多个数字组成的数)某位上的数字是 Y,那么它所表示的数值大小等于 Y × 权重。 怎么理解???看下面实例:
[1] –> 整数部分
例如,将八进制数字 53627(Oct) 转换成十进制:
(八进制)53627 = 5×8^4 + 3×8^3 + 6×8^2 + 2×8^1 + 7×8^0 = 22423(十进制)
从右往左看,第 1 位的位权为 8^0=1,第 2 位的位权为 8^1=8,第 3 位的位权为 8^2=64,第 4 位的位权为 8^3=512,第 5 位的位权为 8^4=4096 …… 第 n 位的位权就为 8^(n-1)。将各个位的数字乘以位权,然后再相加,就得到了十进制形式。
再如,将十六进制数字 9FA8C(Hex) 转换成十进制:
(十六进制)9FA8C = 9×16^4 + 15×16^3 + 10×16^2 + 8×16^1 + 12×16^0 = 653964(十进制)
从右往左看,第 1 位的位权为 16^0=1,第 2 位的位权为 16^1=16,第 3 位的位权为 16^2=256,第 4 位的位权为 16^3=4096,第 5 位的位权为 16^4=65536 …… 第 n 位的位权就为 16^(n-1)。将各个位的数字乘以位权,然后再相加,就得到了十进制形式。
将二进制数字 11010(B) 转换成十进制也是类似的道理:
(二进制)11010 = 1×2^4 + 1×2^3 + 0×2^2 + 1×2^1 + 0×2^0 = 26(十进制)
从右往左看,第 1 位的位权为 2^0=1,第 2 位的位权为 2^1=2,第 3 位的位权为 2^2=4,第 4 位的位权为 2^3=8,第 5 位的位权为 2^4=16 …… 第 n 位的位权就为 2^(n-1)。将各个位的数字乘以位权,然后再相加,就得到了十进制形式。
[2] –> 小数部分
例如,将八进制数字 423.5176 转换成十进制:
(八进制)423.5176 = 4×8^2 + 2×8^1 + 3×8^0 + 5×8^(-1) + 1×8^(-2) + 7×8^(-3) + 6×8^(-4) = 275.65576171875(十进制)
小数部分和整数部分相反,要从左往右看,第 1 位的位权为 8^(-1)=1/8,第 2 位的位权为 8^(-2)=1/64,第 3 位的位权为 8^(-3)=1/512,第 4 位的位权为 8^(-4)=1/4096 …… 第 m 位的位权就为 `8^(-m)。
再如,将二进制数字 1010.1101 转换成十进制:
(二进制)1010.1101 = 1×2^3 + 0×2^2 + 1×2^1 + 0×2^0 + 1×2^(-1) + 1×2^(-2) + 0×2^(-3) + 1×2^(-4) = 10.8125(十进制)
小数部分和整数部分相反,要从左往右看,第 1 位的位权为 2^(-1)=1/2,第 2 位的位权为 2^(-2)=1/4,第 3 位的位权为 2^(-3)=1/8,第 4 位的位权为 2^(-4)=1/16 …… 第 m 位的位权就为 2^(-m)。
将十进制转换为二进制、八进制、十六进制
将十进制转换为其它进制时比较复杂,整数部分和小数部分的算法不一样,分别讲解:
[1] –> 整数部分
十进制整数转换为 N 进制 整数采用 “除 N 取余,逆序排列”法。具体做法是:
- 将 N 作为除数,用十进制整数除以 N,可以得到一个商和余数;
- 保留余数,用商继续除以 N,又得到一个新的商和余数;
- 仍然保留余数,用商继续除以 N,还会得到一个新的商和余数;
- ……
- 如此反复进行,每次都保留余数,用商接着除以 N,直到商为 0 时为止。
演示将十进制数字 36926 转换成八进制的过程 >>>>
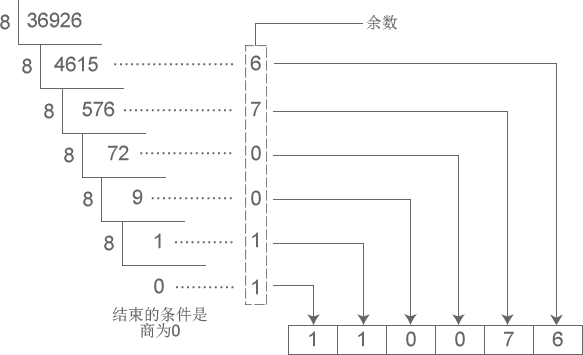
从图中得知,十进制数字 36926 转换成八进制的结果为 110076。
演示将十进制数字 42 转换成二进制的过程 >>>>
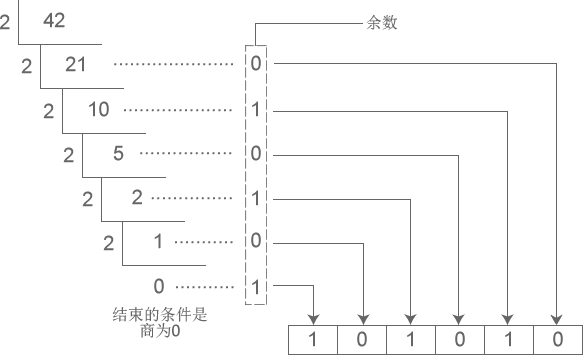
从图中得知,十进制数字 42 转换成二进制的结果为 101010。
[2] –> 小数部分
十进制小数转换成 N 进制 小数采用“乘 N 取整,顺序排列”法。具体做法是:
- 用 N 乘以十进制小数,可以得到一个积,这个积包含了整数部分和小数部分;
- 将积的整数部分取出,再用 N 乘以余下的小数部分,又得到一个新的积;
- 再将积的整数部分取出,继续用 N 乘以余下的小数部分;
- ……
- 如此反复进行,每次都取出整数部分,用 N 接着乘以小数部分,直到积中的小数部分为 0,或者达到所要求的精度为止。
演示将十进制小数 0.930908203125 转换成八进制小数的过程 >>>>
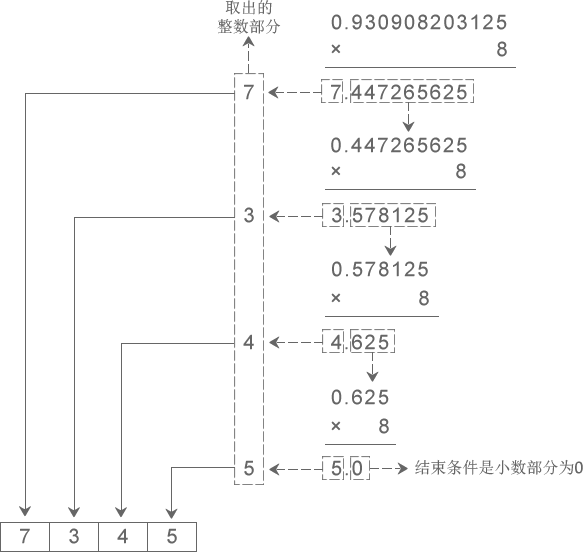
从图中得知,十进制小数 0.930908203125 转换成八进制小数的结果为 0.7345。
演示将十进制小数 0.6875 转换成二进制小数的过程 >>>>
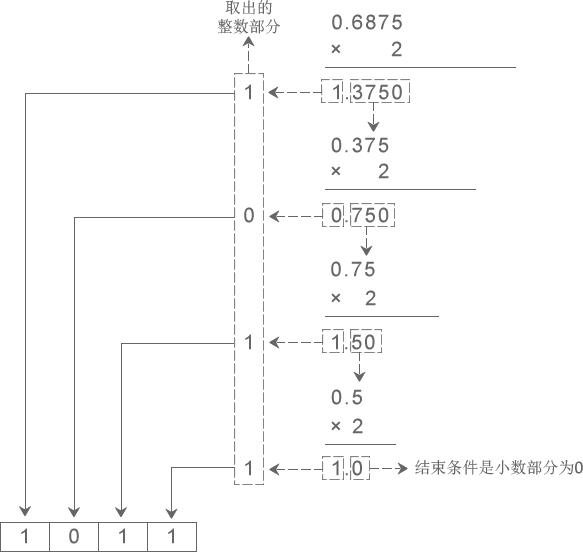
从图中得知,十进制小数 0.6875 转换成二进制小数的结果为 0.1011。
[3] –> 整数部分 && 小数部分
如果一个数字既包含了整数部分又包含了小数部分,那么将整数部分和小数部分开,分别按照上面的方法完成转换,然后再合并在一起即可。例如:
- 十进制数字
36926.930908203125转换成八进制的结果为110076.7345; - 十进制数字
42.6875转换成二进制的结果为101010.1011。
将十进制数转化为其它进制数无限问题
十进制小数转换成其他进制小数时,结果有可能是一个无限位的小数。
请看下面的例子:
- 十进制
0.51对应的二进制为0.100000101000111101011100001010001111010111...,是一个循环小数; - 十进制
0.72对应的二进制为0.1011100001010001111010111000010100011110...,是一个循环小数; - 十进制
0.625对应的二进制为0.101,是一个有限小数。
但我们知道,计算机内存有限,我们不能用储存所有的小数位数。那么在精度与内存间如何取舍呢???
答案是:在某个精度点直接舍弃,代价就是,计算机内部相应数值不是精准的。
十进制小数在高级程序设计语言中属于浮点类型数据,既然十进制小数存储到内存中有误差,所以计算机中的浮点型数值的计算是不精确的,这种问题 对于所有支持浮点数运算的编程语言都是存在的。
导致什么问题??? >>>> 永远不要直接比较两个浮点的大小!!! >>>> 0.1 + 0.2 不等于 0.3(传送门 –> 为什么 0.1 + 0.2 不等于 0.3?)。
但我们知道:
实际应用中,不同行业,要求的精度不是线性的,我们允许(对结果无关紧要的)误差存在。 10.0001 与 10.001 在铁路工程师看来都是合格的。
二进制和八进制、十六进制的转换
将二进制转换为八进制和十六进制时非常简洁,反之亦然。
[1] –> 二进制整数和八进制整数之间的转换
1)二进制 >>>> 八进制
二进制整数转换为八进制整数时,每三位二进制数字转换为一位八进制数字,高位不足三位用零补齐,注意从低位向高位依次进行。
下图演示如何将二进制整数 1 110 111 100 转换为八进制:
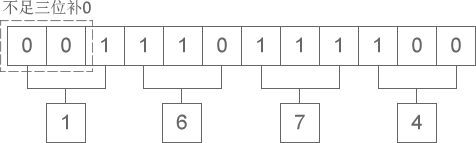
从图中可以看出,二进制整数 1 110 111 100 转换为八进制的结果为 1674。
2)八进制 >>>> 二进制
八进制整数转换为二进制整数时,思路是相反的,每一位八进制数字转换为三位二进制数字,注意从低位向高位依次进行。
下图演示了如何将八进制整数 2743 转换为二进制:
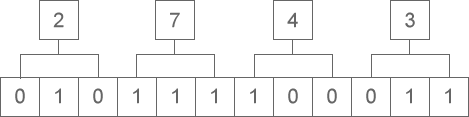
从图中可以看出,八进制整数 2743 转换为二进制的结果为 10 111 100 011。
[2] –> 二进制整数和十六进制整数之间的转换
1)二进制 >>>> 十六进制
二进制整数转换为十六进制整数时,每四位二进制数字转换为一位十六进制数字,高位不足四位用零补齐,注意从低位向高位依次进行。
下图演示了如何将二进制整数 10 1101 0101 1100 转换为十六进制:
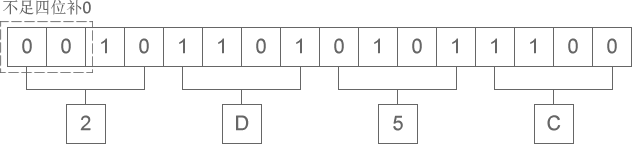
从图中可以看出,二进制整数 10 1101 0101 1100 转换为十六进制的结果为 2D5C。
2)十六进制 >>>> 二进制
十六进制整数转换为二进制整数时,思路是相反的,每一位十六进制数字转换为四位二进制数字,注意从低位向高位依次进行。
下图演示了如何将十六进制整数 A5D6 转换为二进制:

从图中可以看出,十六进制整数 A5D6 转换为二进制的结果为 1010 0101 1101 0110。
八进制和十六进制的转换
八进制和十六进制之间也极少直接转换。
而且,八进制和十六进制之间转换: 可先其转换为十进制数,再由在十进制数转换为十六进制或者八进制。
install_url to use ShareThis. Please set it in _config.yml.