Python 数据分析之 NumPy 数学计算库

  Data Analysis2 hours read (About 19916 words)

NumPy 是 Numerical Python 的缩写，它是 Python 语言的一个第三方数值计算库，用于弥补 Python 对多维数组和矩阵运算的支持。其地位斐然，是 Python 进行科学计算、数据分析以及机器学习的基础包，必须掌握不可！！！

话不多说，一睹为快~~~

更多 Python 数据分析扩展相关内容，请关注博主相关博文系列 ↓↓↓↓↓

之一 >>>> Python 数据分析之 NumPy 数学计算库

之二 >>>> Python 数据分析之 Pandas 数据分析库

之三 >>>> Python 数据分析之 Matplotlib 数据可视化库

之四 >>>> Python 数据分析之 SciPy 科学计算化库

Introduction

NumPy（Numerical Python）是 Python 语言的一个扩展数值计算库，支持多维数组和矩阵运算，此外针对数组运算提供了大量的数学函数支持。再加上其底层主要用 C 语言编写，因此可以高速地执行数组与矩阵的数值计算。

见面知义，NumPy 是专门面向 Python 的数值计算库，其特点就在于 >>> 扩充了 Python 对多维数组和矩阵运算的支持，提供了更丰富的数学函数。

👇👇👇 数组（Array）VS 矩阵（Matrix） 👇👇👇

↓↓↓↓↓↓ 数组（Array） ↓↓↓↓↓↓

  • 数组（Array）是有限个、数据类型相同的元素，组成的元素序列；
  • 数组（Array）中的每个元素都是数组的一个分量，都有一个对应的下标（索引）；

↓↓↓↓↓↓ 矩阵（Matrix） ↓↓↓↓↓↓

  • 矩阵（Matrix）是一个由实数或复数元素排列而成的长方阵列；
  • 矩阵（Matrix）最早来自于方程组的系数以及常数构成的方阵。

↓↓↓↓↓↓ 数组和矩阵的区别 ↓↓↓↓↓↓

  • 矩阵（Matrix）中的元素只能是数字，而数组（Array）中的元素还可以是字符串等；
  • 矩阵（Matrix）是二维的，而数组（Array）可以是一维的、多维的；
  • 矩阵（Matrix）显示时，元素之间无逗号；而数组（Array）显示时，元素之间用逗号隔开。

| =============================================== Split Line ================================================= |

👇👇👇 应用场景 👇👇👇

NumPy 通常与 SciPy（科学计算或算法库）、Pandas（数据分析库）和 Matplotlib（数据可视化库）一起使用，该组合广泛用于替代 MatLab，进行数据分析以及机器学习任务。

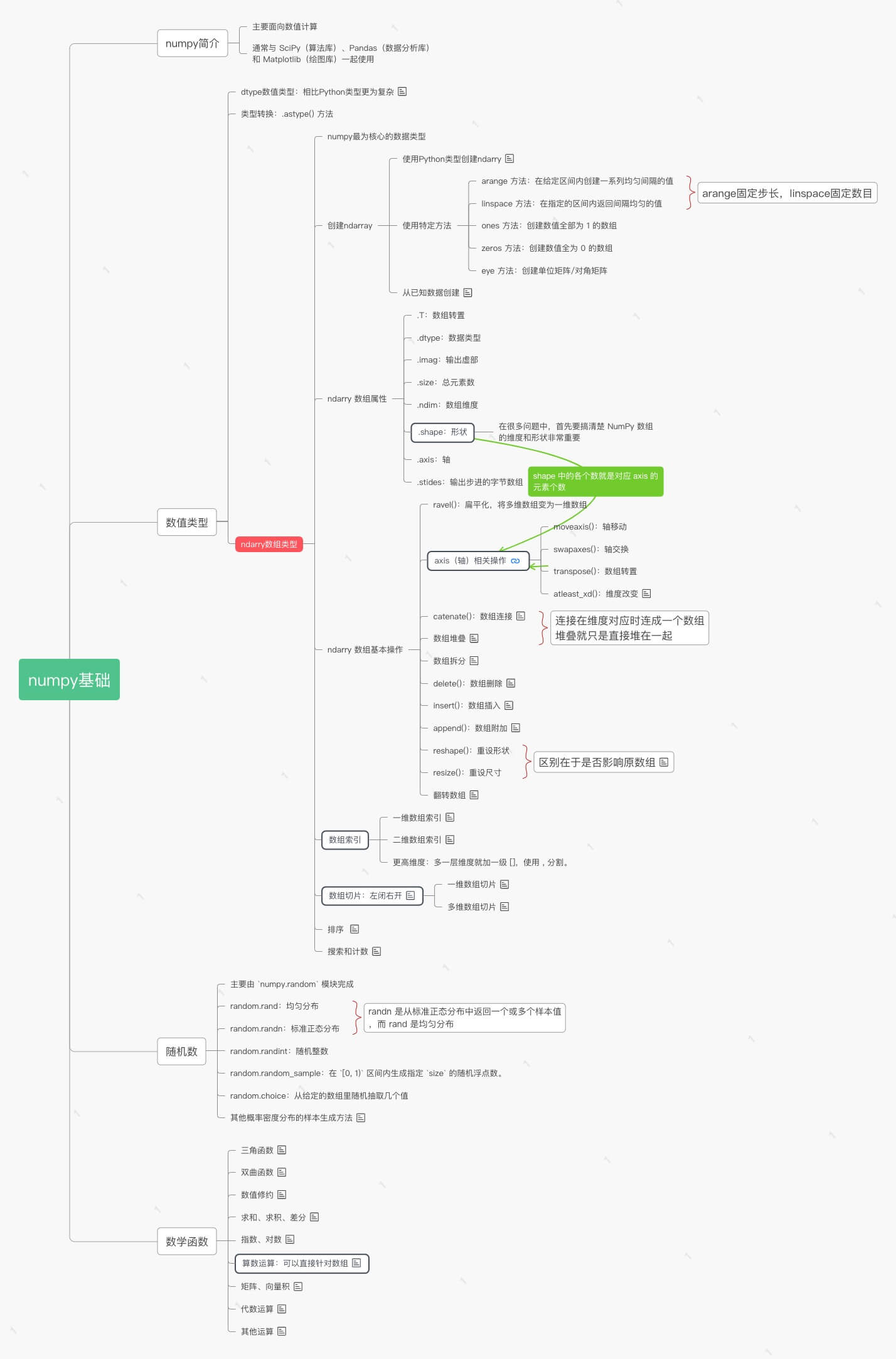
NumPy 知识点思维导图一览：

Setup && Import

我们知道，NumPy 是 Python 的第三方扩展包，不包含在 Python 的内置库中，因此需要单独安装它。

↓↓↓↓↓↓ 1. Setup ↓↓↓↓↓↓

NumPy 的安装方式也比较简单，直接使用 Python 的包管理器 pip 进行安装即可：

1
$ pip install numpy

由于 NumPy 通常与 SciPy && Pandas && Matplotlib 库组合使用，它们均可以使用包管理器 pip 直接安装：

1
2
3
$ pip install scipy
$ pip install pandas
$ pip install matplotlib

需要注意的是，Windows 下直接使用 pip install scipy 可能会发生依赖项报错问题，所以不推荐直接使用 Python 原生 pip 安装 SciPy 程序包。

推荐使用 Anaconda 科学计算平台提供的 Conda 工具进行安装（很好的解决 Windows 平台安装第三方包经常失败的场景），详情可参见 >>> 【一文了解数据科学神器 Anaconda】。

↓↓↓↓↓↓ 2. Import ↓↓↓↓↓↓

NumPy 使用前，可以根据使用情况选择 numpy 包的导入方式：

1
2
3
4
5
6
# 将整个模块导入
import numpy
# 方便模块使用（常用）
import numpy as np
from numpy import *
from numpy import array, sin

之后的学习中，你可能还会在 Jupyter（或 IPython）中看到如下导入方式（Magic 指令）：

1
2
3
4
# 不推荐该导入方式：
%pylab
Using matplotlib backend: <object object at 0x000002849FB94E60>
Populating the interactive namespace from numpy and matplotlib

根据日志信息，发现该魔法指令同时导入了 numpy && matplotlib，如何理解？！！官网有这样一段描述：

1
pylab is a convenience module that bulk imports matplotlib.pyplot (for plotting) and numpy (for mathematics and working with arrays) in a single name space. Although many examples use pylab, it is no longer recommended.

这是 stackoverflow 上的解释 >>> 【What is the difference between pylab and pyplot?】。

NumPy Ndarray 数组

为什么说 NumPy 数组是对 Python 多维数组的扩展？？？Python 内建对象中，数组的两种形式：

  • 列表：[1, 2, 3]
  • 元组：(1, 2, 3, 4, 5)

可见，Python 标准类针对数组的直接处理局限于 1 维~~~

NumPy 数值计算库的核心特性 就是 >>>> 定义了一个 n 维数组对象，ndarray 对象。NumPy 数组也就是 ndarray 多维数组 <<<< 区别于 Python 标准库，NumPy 拥有对高维数组的直接处理能力。

Ndarray 对象结构解析

通俗的来说：

ndarray 数组是 >>> 由 相同数据类型的元素 组成的元素序列，且每个元素均有一个对应下标（索引机制）。数组的索引机制将 元素序列都映射到内存块（连续的内存空间） 中，并按照一定的 布局方式（C-Order：行优先 && Fortran-Order：列优先）对内存块进行排列。

你可以结合 ndarray 的内存布局示意图理解：

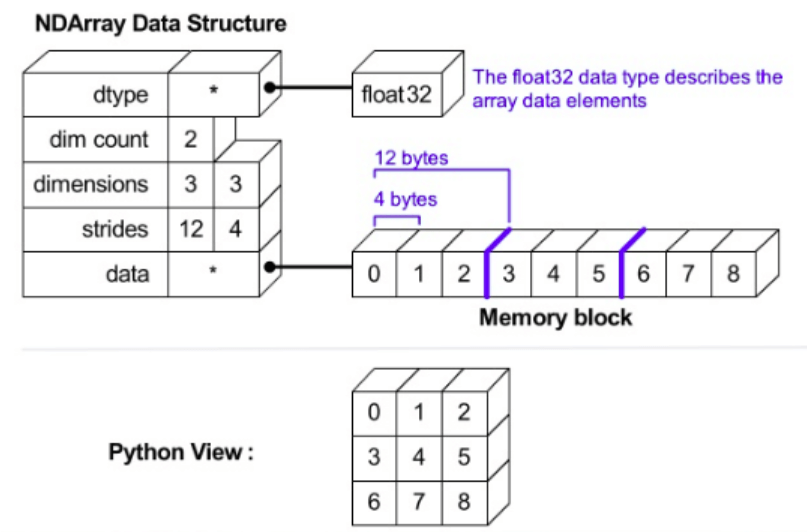
其中：

  • dtype：数据类型 >>> 指定了数组中每个元素占用多少个字节，这几个字节怎么解释（例如：int32、float32 等 NumPy 数据类型）；
  • ndim（dim count）：数组维度（数值） >>> 数组有多少维；
  • shape（dimensions）：数组形状（元组） >>> 每个维度上的元素数量；
  • strides：维间距或步幅（元组） >>> 到达当前维下一个相邻数据需要前进的字节数；
  • data：数组所对应的元素序列（数据） >>> 存放于连续的 Memory Block 中。

篇幅原因，关于 ndarray 对象的更进一步说明，可参见 >>>> 【一文解析 NumPy ndarray 多维数组结构设计】。

在创建 ndarray 多维数组之前，需要先了解一下数组中元素数值的数据类型支持，才能更合理、高效的创建和使用 NumPy 数组：

NumPy 数据类型支持

作为专门的数值计算库，NumPy 支持比 Python 更加丰富的数值类型（Number）：

Num 数据类型 描述
1 bool_ 布尔型数据类型（True 或者 False），1 字节
2 int_ 默认整数类型，类似于 C 语言中的 long，取值为 int32 或 int64
3 intc 和 C 语言的 int 类型一样，一般是 int32 或 int 64
4 intp 用于索引的整数类型（类似于 C 的 ssize_t，通常为 int32 或 int64）
5 int8 代表 1 字节（8bit）整数（-128 ~ 127）
6 int16 代表 2 字节（16it）的整数 （-32768 ~ 32767）
7 int32 代表 4 字节（32bit）整数（-2147483648 ~ 2147483647）
8 int64 代表 8 字节（64bit）整数（-9223372036854775808 ~ 9223372036854775807）
9 uint8 代表 1 字节（8bit）无符号整数（0 ~ 255）
10 uint16 代表 2 字节（16it）无符号整数（0 ~ 65535）
11 uint32 代表 4 字节（32it）无符号整数（0 ~ 4294967295）
12 uint64 代表 8 字节（64it）无符号整数（0 ~ 18446744073709551615）
13 float_ float64 类型简写
14 float16 半精度浮点数，包括：1 个符号位，5 个指数位，10 个尾数位
15 float32 单精度浮点数，包括：1 个符号位，8 个指数位，23 个尾数位
16 float64 双精度浮点数，包括：1 个符号位，11 个指数位，52 个尾数位
17 complex_ complex128 类型简写
18 complex64 表示实部和虚部共享 32 位的复数
19 complex128 表示实部和虚部共享 64 位的复数
19 str_ 字符串类型
20 string_ 字节串类型

dtype Object

事实上，上述所有的数据类型，均属于 NumPy 数据类型对象（Data Type Object）的实例，也称为 dtype Object 实例。

dtype 对象主要用来描述数组中元素的数据类型（整型、浮点或者 Python 对象）、数据大小（占用多少字节），以及字节顺序等。可以为 ndarray 数组中元素数值指定数据类型。其构建语法如下：

1
numpy.dtype(object)

来看一个实例：

1
2
3
4
5
6
7
8
9
10
# 导入 NumPy 模块：
import numpy as np

# 构建一个 dtype 对象：
dt= np.dtype(np.int64)  # 或 dt= np.dtype('int64')
print(dt)  # 输出：dtype('int64')

# 为一个 ndarray 对象指定数据类型（np.array 函数使用可参见后文）：
a = np.array([1, 2, 3], dtype=dt)  # np.array 函数的 dtype 参数可用于指定创建数组时的数据类型
print(a)  # 输出：array([1, 2, 3], dtype=int64)

↓↓↓↓↓↓ 如何检查 ndarray 数组的数据类型 ↓↓↓↓↓↓

NumPy 数组对象（ndarray）提供有一个名为 dtype 的属性，可返回 ndarray 数组的数据类型

1
2
3
4
5
import numpy as np
a = np.array([1, 2, 3], dtype=np.int64)

# 用于查看数组中元素的数据类型
print(a.dtype)  # 输出：dtype('int64')

数据类型字符标识

Numpy 中数据类型都提供有一个唯一对应的 >>>> 字符标识码，码表如下：

字符 对应类型
b 代表布尔型
i 代表符号整型
u 代表无符号整型
f 代表浮点型
c 代表复数浮点型
m 代表时间间隔（timedelta）
M 代表日期时间（datatime）
O 代表 Python 对象
S,a 代表字节串
U 代表 Unicode 字符串
V 原始数据（void）

使用数据类型对应的字符标识码（字符标识码 + 字节数），可以更快捷地创建 dtype Object。如下（以 Int 为例，其它类似）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
import numpy as np

# 等价于 dt = np.dtype(np.int32)
dt = np.dtype('i4')
# 甚至等价于 dt = np.dtype('int32')
print(dt)
# 输出：dtype('int32')

# 等价于 dt = np.dtype(np.int64)
dt = np.dtype('i8')
# 甚至等价于 dt = np.dtype('int64')
print(dt)
# 输出：dtype('int64')

# 等价于 dt = np.dtype(np.float32)
dt = np.dtype('f4')
# 甚至等价于 dt = np.dtype('float32')
print(dt)
# 输出：dtype('float32')

结构化数据类型

先来看一个样例：

1
2
3
4
5
6
7
8
9
10
11
import numpy as np

# 使用 NumPy 内置数据类型 np.int64 创建 ndarray 数组：
a = np.array([1, 2, 3], dtype=np.int64)
print(a.dtype)  # 输出：dtype('int64')

b = np.array([4, 5, 6], dtype='float32')
print(b.dtype)  # 输出：dtype('float32')

c = np.array([7, 8, 9], dtype='u2')
print(c.dtype)  # 输出：dtype('uint16')

最开始的实例中，我们使用 numpy.dtype 对象来为 ndarray 数组指定数据类型。而本节样例中发现可以使用更便捷的方式指定数组中元素的数据类型。

那么，这里产生一个问题 >>>> 使用 dtype 对象会使得 ndarray 数组的创建复杂度进一步提高。

事实上，我们更多的使用 dtype 对象在 定义结构化数据类型 的场景。

通过情况下， 结构化数据使用字段的形式来描述某个对象的特征。例如描述一位老师的姓名、年龄、工资的特征，该结构化数据（老师）其包含以下字段：

  • name：string 字段
  • age：int 字段
  • salary：float 字段

那么，如何基于 dtype 对象 来定义上述结构化数据类型？！！如下（字段名 + 字段数据类型）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
import numpy as np

# 构造结构化数据类型 teacher：
teacher = np.dtype([('name', 'S20'), ('age', 'i1'), ('salary', 'f4')])
# teacher = np.dtype([('name', 'a20'), ('age', 'i1'), ('salary', 'f4')])
print(teacher)
# 输出：[('name', 'S20'), ('age', 'i1'), ('salary', '<f4')]

# 应用于 ndarray 数组对象：
b = np.array([('ycs', 32, 6357.50),('jxe', 28, 6856.80)], dtype = teacher)
print(b)
# 输出：[(b'ycs', 32, 6357.5) (b'jxe', 28, 6856.8)]
print(b.dtype)
# 输出：dtype([('name', 'S20'), ('age', 'i1'), ('salary', '<f4')])

↓↓↓↓↓↓↓ 使用字段名获取数组中所有元素当前字段值列表 ↓↓↓↓↓↓↓ 

1
2
3
4
5
6
7
8
9
10
11
12
import numpy as np
dt = np.dtype([('score','i1')])
print(dt)
# 输出：[('score', 'i1')]

a = np.array([(60,), (75), (90)], dtype=dt)
print(a)
# 输出：[(60,) (75,) (90,)]
print(a.dtype)
# 输出：[('score', 'i1')]
print(a['score'])
# 输出：[60 75 90]

数据类型转换

ndarray 数组对象提供了一个 astype 函数，用于创建数组副本，并将参数指定为数组副本的数据类型。

实例如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
import numpy as np

arr = np.array([1.1, 2.2, 3.3])
print(arr.dtype)
# float64

newarr = arr.astype('i')
print(newarr)
# [1 2 3]
print(newarr.dtype)
# int32

# 其它形式：
newarr = arr.astype(np.int8)
print(newarr.dtype)
# int8
newarr = arr.astype(np.dtype('int16'))
print(newarr.dtype)
int16

如果数组（列表、元组）中元素存在的字符串均为数值型字符串，是可以使用数值类型进行 ndarray 对象创建的，并且可以进行数值类型转化。

1
2
3
4
5
6
7
8
9
import numpy as np
arr_a = np.array([1.1, 2.2, 3.3, '5'], dtype='float32')

print(arr_a)
# [1.1 2.2 3.3 5. ]
print(arr_a.dtype)
# float32

# ValueError: arr_a = np.array([1.1, 2.2, 3.3, 'a'], dtype='float32')

需要注意的是 >>> 当占用字节较多的数据（int32）类型转化为较少字节数据（int8）类型时，如果数值超过小字节数据类型时，会被截断。

👇👇👇 关于 dtype Object 字节序 👇👇👇

字节顺序取决于数据类型的前缀是 < 还是 >。其中（看开口）：

  • < : 小端序(Small-Endian)：低地址存放低字节，高地址存放高字节；

  • > : 大端序(Big-Endian)：高地址存放低字节，低地址存放高字节.

来看一个实例：

1
2
3
4
5
6
7
import numpy as np

a = np.array([1, 2, 3], dtype='>f4')
print(a)
# [1. 2. 3.]
>>> print(a.dtype)
# >f4

Ndarray 数组创建

NumPy 中创建 ndarray 类型的方法主要有五类（常用高亮）：

  • 从 Python 数组结构列表，元组等转换；
  • 使用 NumPy 原生方法，例如：numpy.empty && np.ones && np.zeros && np.arange 等；
  • 从存储空间读取数组，例如文本或二进制文件；
  • 使用字符串或缓冲区从原始字节中创建；
  • 使用特殊函数，如 random。

下面分别来看这些常用的创建方法：

使用 Python 内置类型构建

NumPy 中提供了一个 numpy.array 函数，可以将列表（List）或元组（Tuple）转化为 ndarray 数组。其语法格式如下：

1
numpy.array(object, dtype=None, copy=True, order=None, subok=False, ndmin=0)

其中，参数（常用高亮）：

  • object：列表、元组、矩阵；
  • dtype：数组元素的数据类型（如果没有给出，将被确定为保持序列中的对象所需的最小类型）；
  • ndmin：生成的数组应具有的最小维数，可根据需要预先设置维度；
  • order：数组的内存布局，常见为 C-Order（行优先） && Fortran-Order（列优先）；默认为 K，以尽可能接近数组元素在内存中出现的顺序；
  • copy：布尔类型，默认 True，表示复制对象；否则，只有当 __array__ 返回副本，obj 是嵌套序列，或者需要副本来满足任何其他要求（dtype，顺序等）时，才会进行复制；
  • subok：布尔类型，表示子类是否被传递，True 为（传递）；否则不传递，返回的数组将被强制为基类数组（默认）。

实例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
>>> import numpy as np

# 一维数组：
>>> np.array([1, 2, 3])
array([1, 2, 3])

# 二维数组：
>>> np.array([[1, 2, 3], [4, 5, 6]])
array([[1, 2, 3],
       [4, 5, 6]])
>>> np.array([(1, 2, 3), (4, 5, 6)])
array([[1, 2, 3],
       [4, 5, 6]])

# 最小维度为 2：
>>> np.array([1, 2, 3], ndmin=2)
array([[1, 2, 3]])

# 指定类型：
>>> np.array([1, 2, 3], dtype=np.float32)
array([1., 2., 3.], dtype=float32)

# 结构化类型数据：
>>> np.array([(1, 2), (3, 4)], dtype=np.dtype([('a', 'i1'), ('b', 'i4')]))
array([(1, 2), (3, 4)], dtype=[('a', 'i1'), ('b', '<i4')])
>>> np.array([(5, 6), (7, 8)], dtype=[('a', 'i1'), ('b', 'i4')])
array([(5, 6), (7, 8)], dtype=[('a', 'i1'), ('b', '<i4')])

# 从子类创建数组（是否传递子类）：
>>> np.array(np.mat('1 2; 3 4'))
array([[1, 2],
       [3, 4]])
>>> np.array(np.mat('1 2; 3 4'), subok=True)
matrix([[1, 2],
        [3, 4]])

| ============================================== numpy.asarray ============================================== |

类似于 numpy.array，numpy.asarray 函数，也是将列表（List）或元组（Tuple）等序列转化为 ndarray 数组.

但其使用更为简单。语法格式如下：

1
numpy.asarray(sequence，dtype=None，order=None)

其中，参数：

  • sequence：列表、元组、嵌套列表或元组；
  • dtype：数组元素的数据类型；
  • order：数组的内存布局，参上。

实例如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
>>> import numpy as np

# Use List：
>>> list1 = [1, 2, 3, 4, 5]
>>> arr = np.asarray(list1)
>>> type(arr)
<class 'numpy.ndarray'>
>>> arr
array([1, 2, 3, 4, 5])

# Use Tuple：
>>> tuple1 = (6, 7, 8, 9, 0)
>>> arr = np.asarray(tuple1)
>>> type(arr)
<class 'numpy.ndarray'>
>>> arr
array([6, 7, 8, 9, 0])


>>> list_tp = [(1, 2), (3, 4), (5, 6)]
>>> arr = np.asarray(list_tp)
>>> type(arr)
<class 'numpy.ndarray'>
>>> arr
array([[1, 2],
       [3, 4],
       [5, 6]])

👇👇👇 其它 as 方法 👇👇👇

NumPy 中还提供有其它以 as 开头的构建方法，可以将特定输入转化为数组、矩阵、标量等：

  • asanyarray(a，dtype，order)：将特定输入转换为 ndarray；
  • asfarray(a，dtype)：将特定输入转换为 float 类型的数组；
  • asarray_chkfinite(a，dtype，order)：将特定输入转换为数组，并检查元素 NaN 或 infs；
  • asmatrix(data，dtype)：将特定输入转换为矩阵；
  • asscalar(a)：将大小为 1 的数组转换为标量。

使用 Numpy 原生方法构建

根据生成数组中的元素是否有规律，将要介绍的原生方法分为三类：

  1. 通用数组：numpy.zeros && numpy.ones && numpy.full && numpy.empty；
  2. 特殊数组：numpy.eye；
  3. 区间数组：numpy.arange && numpy.linspace && numpy.logspace。

1 >>>> 通用数组构建

↓↓↓↓↓↓ 1.numpy.zeros ↓↓↓↓↓↓

numpy.zeros 函数用于 快速创建数值全部为 0 的多维数组（可同时指定数组的形状和类型），其语法格式如下：

1
numpy.ones(shape, dtype=float, order='C')

其中，shape 是指数组的形状，即每一维度上的元素数量。默认类型为 float64，其它参数见上文说明。

实例：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
>>> import numpy as np

>>> arr = np.zeros((3, 2))
# 默认类型为：`float64`
>>> arr.dtype
dtype('float64')
# 数组中元素值被初始化为：0
>>> arr
array([[0., 0.],
       [0., 0.],
       [0., 0.]])

# 也可以使用自定义的数据类型构建：
>>> arr = np.zeros((3, 2), dtype=[('x', 'i1'), ('y', 'i1')])
>>> arr
array([[(0, 0), (0, 0)],
       [(0, 0), (0, 0)],
       [(0, 0), (0, 0)]], dtype=[('x', 'i1'), ('y', 'i1')])

↓↓↓↓↓↓ 2.numpy.ones ↓↓↓↓↓↓

numpy.ones 函数和 numpy.zeros非常相似，唯一区别在于数组元素的初始值为 1，其语法格式如下：

1
numpy.ones(shape, dtype=float, order='C')

参数说明见上文，实例如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
>>> import numpy as np

>>> arr = np.ones((3, 2))
# 默认类型为：`float64`
>>> arr.dtype
dtype('float64')
>>> arr
array([[1., 1.],
       [1., 1.],
       [1., 1.]])

# 也可以使用自定义的数据类型构建：
>>> arr = np.ones((2, 2), dtype=[('x', 'i1'), ('y', 'i1')])
>>> arr
array([[(1, 1), (1, 1)],
       [(1, 1), (1, 1)]], dtype=[('x', 'i1'), ('y', 'i1')])

↓↓↓↓↓↓ 3.numpy.full ↓↓↓↓↓↓

类似于 numpy.ones && numpy.zeros，可用于 快速创建数值全部为 某固定值（fill_value）的多维数组（可同时指定数组的形状和类型），其语法格式如下：

1
numpy.full(shape, fill_value, dtype=None, order='C')

参数说明见上文，实例如下：

1
2
3
4
5
6
7
>>> import numpy as np

>>> arr = np.full((3, 2), 2)
>>> arr
array([[2, 2],
       [2, 2],
       [2, 2]])

↓↓↓↓↓↓ 4.numpy.empty ↓↓↓↓↓↓

类似于 numpy.ones && numpy.zeros，区别是 >>> 不会初始化数组中元素（垃圾值，无意义），它要求用户人为地给数组中的每一个元素赋值（谨慎使用）。

其语法格式如下：

1
numpy.empty(shape, dtype=float, order='C')

参数说明见上文，实例如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
>>> import numpy as np

>>> arr = np.empty((2, 2))
# 默认类型为：`float64`
>>> arr.dtype
dtype('float64')
>>> arr
array([[0., 0.],
       [0., 0.]])

# 指定数据类型：
>>> arr = np.empty((2, 2), dtype=int)
>>> arr
array([[-1036147843,  -454467914],
       [  740955874,    58203889]])

# 指定类型为 Python 对象时，元素为 None
>>> arr = np.empty((2, 2), dtype=list)
>>> arr
array([[None, None],
       [None, None]], dtype=object)

| =============================================== Split Line ================================================= |

2 >>>> 特殊数组构建

↓↓↓↓↓↓ 1.numpy.eye ↓↓↓↓↓↓

numpy.eye 可用于创建一个特殊的二维数组，特点是 >>> k 对角线上的值为 1，其余值全部为 0 <<< 可理解为单位矩阵。

其语法格式如下：

1
numpy.eye(N, M=None, k=0, dtype=<type 'float'>, order='C')

其中，参数：N 构造数组的行数；M 是构造数组的列数；而 k 是指主对角线上的值（默认为 1）。

1
2
3
4
5
6
>>> arr = np.eye(4, 4)
>>> arr
array([[1., 0., 0., 0.],
       [0., 1., 0., 0.],
       [0., 0., 1., 0.],
       [0., 0., 0., 1.]])

| =============================================== Split Line ================================================= |

3 >>>> 区间数组构建

所谓的区间数组，是指 >>>> 数组元素的取值位于某个范围内，从而呈现一定的规律。 <<<< 例如：等比数列、递增、递减等。

↓↓↓↓↓↓ 1.numpy.arange ↓↓↓↓↓↓

numpy.arange 函数的功能是 >>> 按照步幅，在给定区间内创建一系列均匀间隔的值（前闭后开的）的 一维 等差数组。其语法格式如下：

1
numpy.arange(start, stop, step, dtype=None)

其中，参数：start && stop 表示元素区间取值范围（前闭后开 >>> [start, stop)）；step 表示步长，值间隔。

实例如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
>>> import numpy as np

>>> arr = np.arange(8)
# 默认数组类型是：int32
>>> arr.dtype
dtype('int32')
>>> arr
# 默认起始范围从 0 开始
array([0, 1, 2, 3, 4, 5, 6, 7])


>>> arr = np.arange(1, 10, 2)
>>> arr
array([1, 3, 5, 7, 9])
# 指定数组类型：
>>> arr = np.arange(1, 10, 2, np.float32)
>>> arr
array([1., 3., 5., 7., 9.], dtype=float32)

↓↓↓↓↓↓ 2.numpy.linspace ↓↓↓↓↓↓

numpy.linspace 函数的功能是 >>> 按照分隔份数，返回均匀间隔的 一维 线性等分数组（等差），默认分隔为 50 份。语法格式如下：

1
numpy.linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None)

其中，参数：

  • start && stop 用于表示元素区间取值范围起始；
  • num 表示要生成的元素数量（份数）；
  • endpoint：表示数列是否包含 stop 终止值（后闭？），默认为 True；
  • retstep：表示生成的数组中是否显示公差项，默认为 False。

实例如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
>>> import numpy as np

# 生成包含 10 个元素的一维等差数组：
>>> arr = np.linspace(1, 10, 10)
>>> arr
array([ 1.,  2.,  3.,  4.,  5.,  6.,  7.,  8.,  9., 10.])

# 设置后开：
>>> arr = np.linspace(1, 10, 10, endpoint=False)
>>> arr
array([1. , 1.9, 2.8, 3.7, 4.6, 5.5, 6.4, 7.3, 8.2, 9.1])

# 设置显示公差：
>>> arr = np.linspace(1, 2, 5, retstep=True)
>>> arr
(array([1.  , 1.25, 1.5 , 1.75, 2.  ]), 0.25)

↓↓↓↓↓↓ 3.numpy.logspace ↓↓↓↓↓↓

类似于 numpy.linspace，numpy.logspace 函数的功能是 >>> 按照分隔份数，返回 一维 对数等分数组（等比），默认分隔为 50 份。语法格式如下：

1
numpy.logspace(start, stop, num=50, endpoint=True, base=10.0, dtype=None)

其中，参数：

  • start && stop 用于表示元素区间取值范围起始；
  • num 表示要生成的元素数量（份数）；
  • endpoint：表示数列是否包含 stop 终止值（后闭？），默认为 True；
  • base：设置 log 底值（公比），默认以 10 为底。

实例如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
>>> import numpy as np

# 生成包含 10 个元素的等比一维数组：
>>> arr = np.logspace(1.0, 2.0, num=10)
>>> arr
array([ 10.        ,  12.91549665,  16.68100537,  21.5443469 ,
        27.82559402,  35.93813664,  46.41588834,  59.94842503,
        77.42636827, 100.        ])

# 生成包含 10 个元素的，公比为 2 的一维等比数组：
>>> arr = np.logspace(1, 10, num=10, base=2)
>>> arr
array([   2.,    4.,    8.,   16.,   32.,   64.,  128.,  256.,  512.,
       1024.])

使用其它方法构建

NumPy 中还支持从字符串或缓冲区、文件以及函数中创建 ndarray 数组：

  • fromstring(string, dtype, count, sep) >>> 从字符串中创建 1 维数组；
  • frombuffer(buffer) >>> 将缓冲区转换为 1 维数组；
  • fromiter(iterable, dtype, count) >>> 从可迭代对象创建 1 维数组；
  • fromfunction(function, shape) >>> 通过函数返回值来创建多维数组；
  • fromfile(file, dtype, count, sep) >>> 从文本或二进制文件中构建多维数组。

Ndarray 数组属性

了解了 ndarray 数组的数据类型支持以及常用构建方法之后，我们需要重新认识一下 ndarray 数组的常用属性。

开始前，首先构建一个二维 ndarray 数组，以便查看其属性：

1
2
3
4
5
6
7
8
>>> import numpy as np
>>> arr = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# 打印：
>>> arr
array([[1, 2, 3],
       [4, 5, 6],
       [7, 8, 9]])

↓↓↓↓↓↓ 数组元素数据类型 ↓↓↓↓↓↓ 

1
2
>>> arr.dtype
dtype('int32')

↓↓↓↓↓↓ 数组元素的实虚部 ↓↓↓↓↓↓ 

1
2
3
4
5
6
7
8
9
10
11
# 实部
>>> arr.real
array([[1, 2, 3],
       [4, 5, 6],
       [7, 8, 9]])

# 虚部
>>> arr.imag
array([[0, 0, 0],
       [0, 0, 0],
       [0, 0, 0]])

↓↓↓↓↓↓ 数组元素总数 ↓↓↓↓↓↓ 

1
2
>>> arr.size
9

↓↓↓↓↓↓ 数组每个元素所占字节数 ↓↓↓↓↓↓ 

1
2
>>> arr.itemsize
4

↓↓↓↓↓↓ 数组中元素总字节数 ↓↓↓↓↓↓ 

1
2
3
4
5
6
>>> arr.nbytes
36

# 或者：
>>> arr.size * arr.itemsize
36

↓↓↓↓↓↓ 数组维度 ↓↓↓↓↓↓ 

1
2
>>> arr.ndim
2

↓↓↓↓↓↓ 数组的形状 ↓↓↓↓↓↓

数组的形状，是数组各维度上的元素个数：

1
2
>>> arr.shape
(3, 3)

↓↓↓↓↓↓ 数组的维间距 ↓↓↓↓↓↓

数组的维间距（步幅），到达当前维下一个相邻数据需要前进的字节数：

1
2
>>> arr.strides
(12, 4)

↓↓↓↓↓↓ 数组的转置 ↓↓↓↓↓↓ 

1
2
3
4
5
6
7
8
9
10
>>> arr.T
array([[1, 4, 7],
       [2, 5, 8],
       [3, 6, 9]])

# 同 transpose 函数：
>>> arr.transpose()
array([[1, 4, 7],
       [2, 5, 8],
       [3, 6, 9]])

↓↓↓↓↓↓ 数组的内存信息 ↓↓↓↓↓↓

返回 ndarray 数组的内存信息，例如：ndarray 数组的存储方式，以及是否是其他数组的副本等。

1
2
3
4
5
6
7
8
9
10
11
>>> import numpy as np

>>> x = np.array([1, 2, 3, 4])
>>> x.flags
  C_CONTIGUOUS : True
  F_CONTIGUOUS : True
  OWNDATA : True
  WRITEABLE : True
  ALIGNED : True
  WRITEBACKIFCOPY : False
  UPDATEIFCOPY : False

篇幅原因，关于 ndarray 对象属性的更进一步说明，可参见 >>>> 【一文解析 NumPy ndarray 多维数组结构设计】。

Ndarray 数组维度和形状

NumPy ndarray 数组中非常的重要的两个属性是 >>> 数组的维度（N Dimensions） && 形状（Shape）。

下面给出 1 至 3 维的 ndarray 数组的视图：

其中，1 维数组可以被看作数学中的向量（行向量/列向量），2 维数组可以看作是矩阵，而 3 维数组则是一个数据立方。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
>>> import numpy as np

>>> one_dim_arr = np.array([1, 2, 3, 4])
>>> one_dim_arr
array([1, 2, 3, 4])

>>> two_dim_arr = np.array([[1, 2, 3], [4, 5, 6]])
>>> two_dim_arr
array([[1, 2, 3],
       [4, 5, 6]])

>>> three_dim_arr = np.array([[[1, 2, 3], [3, 4, 5]], [[5, 6, 7], [7, 8, 9]]])
>>> three_dim_arr
array([[[1, 2, 3],
        [3, 4, 5]],

       [[5, 6, 7],
        [7, 8, 9]]])

可以发现，对于多维数组（N）的显示结果和与列表（List）相同，每多嵌套一层，就代表多一个维度（凭借此你可以很轻易的判断出某个 ndarray 数组的维度）。

通过 shape 属性查看 NumPy ndarray 数组的形状：

1
2
>>> one_dim_arr.shape, two_dim_arr.shape, three_dim_arr.shape
((4,), (2, 3), (2, 2, 3))

| ========================================= 👇👇👇 数组重塑 👇👇👇 =========================================== |

和类型一样，ndarray 数组构建之后，数组的维度和形状也是可变的 >>> 数组重塑。

通常，我们所说的数组重塑，更多的指的是 >>> 数组形状的变化 <<< 维度可变，但少变（研究特定问题时）。

NumPy 中提供了一个简单的 numpy.ndarray.reshape 函数用于重塑 ndarray 数组的形状，其语法格式如下：

1
2
3
4
5
numpy.reshape(array, newShape, order='C')

# 或：
# 同理于 NumPy 中 reshape 方法，但更加方便：
numpy.ndarray.reshape(newShape, order='C')

实例如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
>>> import numpy as np

>>> arr = np.array([1, 2, 3, 4, 5, 6])
>>> arr
array([1, 2, 3, 4, 5, 6])

# Reshape >>> (6, 1) -> (3, 2)
>>> newarr = arr.reshape(3, 2)
>>> newarr
array([[1, 2],
       [3, 4],
       [5, 6]])

# Reshape >>> (6, 1) -> (2, 3)
>>> newarr = arr.reshape(2, 3)
>>> newarr
array([[1, 2, 3],
       [4, 5, 6]])

需要注意的是 >>> 修改 ndarray 数组形状的时候， 不能改变数组中元素的个数。如上面数组的形状是 6 * 1（6），可以修改成 3 * 2（6） && 2 * 3（6），修改后仍是 6 个。否则报错：

1
ValueError: cannot reshape array of size 6 into shape (3,3)

关于数组维度的变化，等后续了解了多维数组轴（axis）之后再进行学习（将会在后续章节进行说明）。

Ndarray 数组索引和切片

NumPy Ndarray 数组完整集成了 Python 对于数组的索引语法 array[obj] >>>

并且，随着 obj 的不同，我们可以实现：元素访问、数组切片，以及其它 高级索引 功能。

数组索引

类似于 Python List 的索引方式，你可以通过索引值（从 0 开始依次）来访问 Ndarray 中的特定位置的单个元素，也可以访问多维数组中的行、列、页。

👇👇👇 一维数组索引 👇👇👇

先来构建一个一维数组：

1
2
3
4
>>> import numpy as np
>>> arr1 = np.array([1, 2, 3, 4])
>>> arr1
array([1, 2, 3, 4])

↓↓↓↓↓↓ Picking an element ↓↓↓↓↓↓

此时，你可以通过类似于 List && Tuple 索引的方式，来获取单个元素的值：

1
2
3
4
5
6
# 获取第一个元素的值：
>>> arr1[0]
1
# 获取第三个元素的值：
>>> arr1[2]
3

| =============================================== Split Line ================================================= |

👇👇👇 二维数组索引 👇👇👇

先来构建一个二维数组：

1
2
3
4
5
6
7
>>> arr2 = np.array([[1, 2, 3], 
                     [4, 5, 6],
                     [7, 8, 9]])
>>> arr2
array([[1, 2, 3],
       [4, 5, 6],
       [7, 8, 9]])

↓↓↓↓↓↓ Picking an element ↓↓↓↓↓↓

二维数组可以看作一个矩阵（Matrix），矩阵中元素的位置由它所处的行（Row）和列（Column）组成。故，你需要通过索引 (Row, Col) 来获取数组中的单个元素：

1
2
3
4
5
6
7
# 获取第 3 行，第 2 列对应的值：
>>> arr2[2, 1]
8

# 获取第 1 行，第 3 列对应的值：
>>> arr2[0, 2]
3

↓↓↓↓↓↓ Picking a row or column ↓↓↓↓↓↓

If we can supply a single index, it will pick a row (Row value) ：

1
2
3
# 返回第三行元素组成的数组：
>>> arr2[2]
array([7, 8, 9])

Numpy allows us to select a single columm as well:

1
2
3
# 返回第二列元素组成的数组：
>>> arr2[:, 1]
array([2, 5, 8])

获取列的方法，要使用到切片（: >>> is a full slice, from start to end）。

| =============================================== Split Line ================================================= |

👇👇👇 三维数组索引 👇👇👇

先来构建一个三维数组：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
>>> arr3 = np.array([[[10, 11, 12], [13, 14, 15], [16, 17, 18]],
                     [[20, 21, 22], [23, 24, 25], [26, 27, 28]], 
                     [[30, 31, 32], [33, 34, 35], [36, 37, 38]]])
>>> arr3
array([[[10, 11, 12],
        [13, 14, 15],
        [16, 17, 18]],

       [[20, 21, 22],
        [23, 24, 25],
        [26, 27, 28]],

       [[30, 31, 32],
        [33, 34, 35],
        [36, 37, 38]]])

三维数组，可以看作是由几个矩阵组成的堆（Stack），每一个矩阵均可看作是三维数组的页（Page）。

故数组中元素的位置由它所处的页（Page）、行（Row）和列（Column）组成。故，你需要通过索引 (Page, Row, Col) 来获取数组中的单个元素：

1
2
3
4
5
6
7
# 获取第 3 页中，矩阵的第 1 行，第 2 列对应的值：
>>> arr3[2, 0, 1]
31

# 获取第 2 页中，矩阵的第 2 行，第 3 列对应的值：
>>> arr3[1, 1, 2]
25

也就是说，第一个 index 选中某个矩阵，后两个 index 表示从选中的矩阵中确定某个元素。

↓↓↓↓↓↓ Picking a row or column ↓↓↓↓↓↓

You can access any row or column in a 3D array. There are 3 cases：

Case 1 - specifying the first two indices. In this case, you are choosing the page value (the matrix), and the row value (the row).

This will select a specific row. In this example we are selecting row 2 from matrix 1:

1
2
3
# 获取第 2 页中，矩阵的第 3 行：
>>> arr3[1, 2]
array([26, 27, 28])

Case 2 - specifying the page value (the matrix), and the col value (the column), using a full slice (:) for the row value (the row).

This will select a specific column. In this example we are selecting column 1 from matrix 0:

1
2
3
# 获取第 1 页中，矩阵的第 2 列：
>>> arr3[0, : , 1]
array([11, 14, 17])

Case 3 - specifying the j value (the row), and the k value (the column), using a full slice (:) for the i value (the matrix).

This will create a row by taking the same element from each matrix. In this case we are taking row 1, column 2 from each matrix:

1
2
3
# 获取由不同页（Page：1~3）中某位置（第 2 行，第 3 列）处元素组成的数组：
>>> arr3[:, 1, 2]
array([15, 25, 35])

↓↓↓↓↓↓ Picking a matrix ↓↓↓↓↓↓

Case 1 - If we only specify the page index, numpy will return the corresponding matrix.

In this example we will request matrix 2:

1
2
3
4
5
# 获取第 3 页的矩阵：
>>> arr3[2]
array([[30, 31, 32],
       [33, 34, 35],
       [36, 37, 38]])

Case 2 - if we specify just the row value (using a full slice for the page values)

we will obtain a matrix made from the selected row taken from each plane. In this example we will take row 1:

1
2
3
4
5
# 获取由不同页（Page：1~3）中第 2 行元素组成的矩阵：
>>> arr3[:, 1]
array([[13, 14, 15],
       [23, 24, 25],
       [33, 34, 35]])

Case 3 - if we specify just the k value (using full slices for the i and j values)

we will obtain a matrix made from the selected column taken from each plane. In this example we will take column 0（取到的元素以行的形式排列）:

1
2
3
4
5
# 获取由不同页（Page：1~3）中第 3 列元素组成的矩阵：
>>> arr3[:, :, 0]
array([[10, 13, 16],
       [20, 23, 26],
       [30, 33, 36]])

对于四维以上的多维数组的索引方式同理，这里就不再介绍。

数组切片

You can slice a numpy array is a similar way to slicing a list - except you can do it in more than one dimension.

👇👇👇 一维数组切片 👇👇👇

Slicing a 1D numpy array is almost exactly the same as slicing a list:

1
2
3
4
5
6
7
>>> import numpy as np
>>> arr1 = np.array([1, 2, 3, 4, 5])

# 切片获取索引为 2 ~ 4 直接的所有元素：
>>> b = arr1[1:4]
>>> b
array([2, 3, 4])

The only thing to remember if that (unlike a list) arr1 and b are both looking at the same underlying data (b is a view of the data). So if you change an element in b, arr1 will be affected (and vice versa):

1
2
3
4
5
>>> b[1] = 10
>>> b
array([ 2, 10,  4])
>>> arr1
array([ 1,  2, 10,  4,  5])

| =============================================== Split Line ================================================= |

👇👇👇 二维数组切片 👇👇👇

You can slice a 2D array in both axes to obtain a rectangular subset of the original array. For example:

1
2
3
4
5
6
7
8
9
10
11
12
>>> import numpy as np

>>> arr2 = np.array([[10, 11, 12, 13, 14],
                     [15, 16, 17, 18, 19], 
                     [20, 21, 22, 23, 24], 
                     [25, 26, 27, 28, 29]])

# 切片获取第 2 行后所有行，且第 3 ~ 4 列的元素组成的数组：
>>> arr2[1:, 2:4]
array([[17, 18],
       [22, 23],
       [27, 28]])

This selects rows 1: (1 to the end of bottom of the array) and columns 2:4 (columns 2 and 3).

| =============================================== Split Line ================================================= |

👇👇👇 三维数组切片 👇👇👇

You can slice a 3D array in all 3 axes to obtain a cuboid subset of the original array:

1
2
3
4
5
6
7
8
9
10
11
12
>>> import numpy as np
>>> arr3 = np.array([[[10, 11, 12], [13, 14, 15], [16, 17, 18]],
                     [[20, 21, 22], [23, 24, 25], [26, 27, 28]],
                     [[30, 31, 32], [33, 34, 35], [36, 37, 38]]])

# 切片获取 0 ~ 1 页中，第 2 行后所有行，且第 1 ~ 2 列的元素组成的数组：
>>> arr3[:2, 1:, :2]
array([[[13, 14],
        [16, 17]],

       [[23, 24],
        [26, 27]]])

This selects: page :2 (the first 2 planes) ；rows 1: (the last 2 rows) ；columns :2 (the first 2 columns).

数组高级索引

NumPy 中还提供了使用高级索引方式：整数数组索引、布尔索引，以及花式索引。

需要注意的是 >>> 高级索引返回的是数组的副本（深拷贝），而切片操作返回的是数组视图（浅拷贝）！！！副本和视图的概念可参考【一文解析 NumPy ndarray 多维数组结构设计】。

高级索引中，最常见的就是整数数组索引：

👇👇👇 整数数组索引 👇👇👇

依次看一下一维、二维数组的整数数组索引方式，然后推导 N 维数组：

↓↓↓↓↓↓ 1D Array ↓↓↓↓↓↓

使用整数数组索引可以同时获取多个索引的元素值：

1
2
3
4
>>> import numpy as np
>>> arr1 = np.arange(10)
>>> arr1
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

相较于单个元素索引方式 >>> 多加了一层 []，使用逗号隔开

1
2
>>> arr1[[1, 3, 5]]
array([1, 3, 5])

↓↓↓↓↓↓ 2D Array ↓↓↓↓↓↓

二维数组获取普通索引值和一维不太一样，由两个维度（Row, Col）构成。

故访问二维 Ndarray 中的多个元素值，需要多加一个 []，分别表示行索引数组、列索引数组：

1
2
3
4
5
6
7
8
9
10
11
12
>>> arr2 = np.array([[ 0,  1,  2,  3,  4],
                     [ 5,  6,  7,  8,  9],
                     [10, 11, 12, 13, 14],
                     [15, 16, 17, 18, 19]])
>>> arr2
array([[ 0,  1,  2,  3,  4],
       [ 5,  6,  7,  8,  9],
       [10, 11, 12, 13, 14],
       [15, 16, 17, 18, 19]])

>>> arr2[[1, 2, 3], [0, 2, 4]]
array([ 5, 12, 19])

其中，行索引数组：[1, 2, 3] && 列索引数组：[0, 2, 4]。将行、列索引组合会得到 (1, 0) && (2, 2) && (3, 4)，它们分别对应着输出元素值在原数组中的索引位置。

完成实例：获取上述 4*5 数组中的四个角上元素，它们对应的行索引是 [0,0] 和 [3,3]，列索引是 [0,4] 和 [0,4]:

1
2
3
4
5
6
7
8
9
>>> row_two = np.array([[0, 0], [3, 3]])
>>> col_two = np.array([[0, 4], [0, 4]])
>>> arr2[row_two, col_two]
array([[ 0,  4],
       [15, 19]])

# 或者：
>>> arr2[[0, 0, 3, 3], [0, 4, 0, 4]]
array([ 0,  4, 15, 19])

更复杂一点，你可以将切片使用的 : 或省略号 ... 与整数数组索引结合使用：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
import numpy as np
>>> arr2 = np.array([[ 0,  1,  2],
...               [ 3,  4,  5],
...               [ 6,  7,  8],
...               [ 9, 10, 11]])
>>> arr2
array([[ 0,  1,  2],
       [ 3,  4,  5],
       [ 6,  7,  8],
       [ 9, 10, 11]])

# 2D Slice：
>>> arr2[1:4, 1:3]
array([[ 4,  5],
       [ 7,  8],
       [10, 11]])

# 行使用基础索引，对列使用高级索引
>>> arr2[1:4, [1, 2]]
array([[ 4,  5],
       [ 7,  8],
       [10, 11]])

# 对行使用省略号
>>> arr2[..., 1:]
array([[ 1,  2],
       [ 4,  5],
       [ 7,  8],
       [10, 11]])

↓↓↓↓↓↓ 3D Array ↓↓↓↓↓↓

思考一下，三维数组的整数数组高级索引是什么情况？？？

先分析，我们知道 3D 数组通过索引 (Page, Row, Col) 来获取数组中的单个元素。

故，相较于二维数组，需要多加一个 []，分别表示 >>> 页索引数组、行索引数组、列索引数组，测试一下：

1
2
3
4
5
6
7
8
9
10
11
12
13
>>> arr3 = np.arange(12).reshape(3, 2, 2)
>>> arr3
array([[[ 0,  1],
        [ 2,  3]],

       [[ 4,  5],
        [ 6,  7]],

       [[ 8,  9],
        [10, 11]]])

>>> arr3[[0, 1], [0, 1], [0, 1]]
array([0, 7])

果然~~~

↓↓↓↓↓↓ ND Array ↓↓↓↓↓↓

所以，对于更高维的数组，多一层维度就加一个 []，表示新增维度。

| =============================================== Split Line ================================================= |

👇👇👇 布尔数组索引 👇👇👇

我们可以通过建立一个布尔数组来索引目标数组，通过数组的逻辑运算作为索引，以此找出与布尔数组中值为 True 所对应目标数组中的数据。

以一个二维数组为例来看具体应用：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
>>> import numpy as np

>>> arr = np.array([[ 0,  1,  2],[ 3,  4,  5],[ 6,  7,  8],[ 9, 10, 11]])
>>> arr
array([[ 0,  1,  2],
       [ 3,  4,  5],
       [ 6,  7,  8],
       [ 9, 10, 11]])

# 数组的逻辑运算结果：
>>> arr > 6
array([[False, False, False],
       [False, False, False],
       [False,  True,  True],
       [ True,  True,  True]])

# 查找出满足逻辑运算结果为 True 的索引，所对应的数组元素：
>>> arr[arr > 6]
array([ 7,  8,  9, 10, 11])

具体的应用场景 >>>

↓↓↓↓↓↓ 匹配筛选 ↓↓↓↓↓↓

布尔索引可以实现 >>> 通过列向量中的每个元素的布尔型数值对一个与列向量有着同样行数的矩阵进行符合匹配。而这样的作用，其实是把列向量中布尔值为 True 的相应行向量给抽取了出来。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
>>> import numpy as np

>>> names = np.array(['Bob', 'Joe', 'Will', 'Bob', 'Will', 'Joe', 'Joe'])
>>> names
array(['Bob', 'Joe', 'Will', 'Bob', 'Will', 'Joe', 'Joe'], dtype='<U4')

>>> print(names == 'Joe')
[False  True False False False  True  True]
>>> data = np.random.randn(7, 4)
>>> data
array([[ 1.37105726,  0.643821  , -0.04952524,  0.87843288],
       [-0.73402717,  1.16743508,  1.96971901, -0.961953  ],
       [ 0.52256989,  1.09314884, -1.05628438,  0.61548645],
       [ 0.80319287,  0.7778842 ,  0.64672434, -0.07293975],
       [ 1.19837729,  0.37055356,  0.7436583 ,  1.43116524],
       [-0.95453104,  0.01908647, -0.19713538, -0.86226891],
       [-1.23236429,  1.60928   ,  1.27864806,  1.85035932]])

# 通过数组的逻辑运算作为索引，筛选出布尔值为 True 所对应目标数组中的数据：
>>> data[names == 'Joe']
array([[-0.73402717,  1.16743508,  1.96971901, -0.961953  ],
       [-0.95453104,  0.01908647, -0.19713538, -0.86226891],
       [-1.23236429,  1.60928   ,  1.27864806,  1.85035932]])

↓↓↓↓↓↓ 布尔型数组的切片用法 ↓↓↓↓↓↓ 

1
2
3
4
5
6
7
>>> data[names == 'Joe', 2:]
array([[ 1.96971901, -0.961953  ],
       [-0.19713538, -0.86226891],
       [ 1.27864806,  1.85035932]])

>>> data[names == 'Joe', 3]
array([-0.961953  , -0.86226891,  1.85035932])

↓↓↓↓↓↓ 布尔条件否定用法 ↓↓↓↓↓↓

如果要选择除 Joe 以外的其他值，可以使用 != 或 ~ 对逻辑运算条件进行否定：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
>>> names != 'Joe'
array([ True, False,  True,  True,  True, False, False])

>>> data[names != 'Joe']
array([[ 1.37105726,  0.643821  , -0.04952524,  0.87843288],
       [ 0.52256989,  1.09314884, -1.05628438,  0.61548645],
       [ 0.80319287,  0.7778842 ,  0.64672434, -0.07293975],
       [ 1.19837729,  0.37055356,  0.7436583 ,  1.43116524]])

>>> data[~(names == 'Joe')]
array([[ 1.37105726,  0.643821  , -0.04952524,  0.87843288],
       [ 0.52256989,  1.09314884, -1.05628438,  0.61548645],
       [ 0.80319287,  0.7778842 ,  0.64672434, -0.07293975],
       [ 1.19837729,  0.37055356,  0.7436583 ,  1.43116524]])

↓↓↓↓↓↓ 多布尔条件用法 ↓↓↓↓↓↓

用 & , 或用 | 来选择满足多个布尔条件（Python 中的 and 和 or 在布尔数组中无效）:

1
2
3
4
5
6
7
8
9
10
>>> mask = (names == 'Bob') | (names == 'Joe')
>>> mask
array([ True,  True, False,  True, False,  True,  True])

>>> data[mask]
array([[ 1.37105726,  0.643821  , -0.04952524,  0.87843288],
       [-0.73402717,  1.16743508,  1.96971901, -0.961953  ],
       [ 0.80319287,  0.7778842 ,  0.64672434, -0.07293975],
       [-0.95453104,  0.01908647, -0.19713538, -0.86226891],
       [-1.23236429,  1.60928   ,  1.27864806,  1.85035932]])

↓↓↓↓↓ 修改满足布尔条件数组的值 ↓↓↓↓↓↓ 

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
>>> data[data < 0] = 0
>>> data
array([[1.37105726, 0.643821  , 0.        , 0.87843288],
       [0.        , 1.16743508, 1.96971901, 0.        ],
       [0.52256989, 1.09314884, 0.        , 0.61548645],
       [0.80319287, 0.7778842 , 0.64672434, 0.        ],
       [1.19837729, 0.37055356, 0.7436583 , 1.43116524],
       [0.        , 0.01908647, 0.        , 0.        ],
       [0.        , 1.60928   , 1.27864806, 1.85035932]])

>>> data[names != 'Bob'] = 8
>>> data
array([[1.37105726, 0.643821  , 0.        , 0.87843288],
       [8.        , 8.        , 8.        , 8.        ],
       [8.        , 8.        , 8.        , 8.        ],
       [0.80319287, 0.7778842 , 0.64672434, 0.        ],
       [8.        , 8.        , 8.        , 8.        ],
       [8.        , 8.        , 8.        , 8.        ],
       [8.        , 8.        , 8.        , 8.        ]])

| =============================================== Split Line ================================================= |

👇👇👇 花式索引 👇👇👇

花式索引也可以理解为整数数组索引，但是它们之间又略有不同。实例代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
>>> import numpy as np

>>> arr = np.arange(32).reshape((8, 4))
>>> arr
array([[ 0,  1,  2,  3],
       [ 4,  5,  6,  7],
       [ 8,  9, 10, 11],
       [12, 13, 14, 15],
       [16, 17, 18, 19],
       [20, 21, 22, 23],
       [24, 25, 26, 27],
       [28, 29, 30, 31]])

# 索引数组的元素值与被索引数组的每一行相对应：
>>> arr[[4, 2, 1, 7]]
array([[16, 17, 18, 19],
       [ 8,  9, 10, 11],
       [ 4,  5,  6,  7],
       [28, 29, 30, 31]])

# 倒序索引数组（取行）：
>>> arr[[-4, -2, -1, -7]]
array([[16, 17, 18, 19],
       [24, 25, 26, 27],
       [28, 29, 30, 31],
       [ 4,  5,  6,  7]])

# 多个索引数组的情况下，需要使用 `np.ix_`
>>> arr[np.ix_([1, 5, 7, 2], [0, 3, 1, 2])]
array([[ 4,  7,  5,  6],
       [20, 23, 21, 22],
       [28, 31, 29, 30],
       [ 8, 11,  9, 10]])

# 其中 [1,5,7,2] 代表行索引，而 [0,3,1,2] 表示与行索引相对应的列索引值，也就是行中的元素值会按照列索引值排序。
# 比如，第一行元素，未排序前的顺序是 [4,5,6,7]，经过列索引排序后变成了 [4,7,5,6]。

自此，你已经完成了 NumPy ndarray 多维数组的基础部分内容学习。在开始后续的学习之前，强烈建议阅读 >>>>【一文解析 NumPy ndarray 多维数组结构设计】一文，可以帮助你更好的理解 ndarray 数组，方便后续内容的学习。

Ndarray 数组遍历

类似于 Python 内置数组（Tuple && List…）遍历，你也可以遍历访问 Ndarray 数组中元素：

通用遍历方法

同样类似于 Python 中 List 等序列的遍历方法，使用 for 循环实现 Ndarray 数组元素的遍历：

👇👇👇 一维数组 👇👇👇

1
2
3
4
5
6
7
8
9
10
11
12
13
>>> import numpy as np
>>> one_arr = np.arange(5)
>>> one_arr
array([0, 1, 2, 3, 4])

>>> for item in one_arr:
...     print(item)
...
0
1
2
3
4

可见，for 循环遍历一维数组中所有元素进行输出。

| ================================================== Split Line =============================================== |

👇👇👇 二维数组 👇👇👇

同样的，可以对二维数组进行遍历：

1
2
3
4
5
6
7
8
9
10
>>> two_arr = np.arange(6).reshape(2, 3)
>>> two_arr
array([[0, 1, 2],
       [3, 4, 5]])

>>> for r in two_arr:
...     print(r)
...
[0 1 2]
[3 4 5]

可见，单层 for 循环会将每行元素组成的一维数组作为一个二维数组的元素，输出三个一维数组。故你可以使用多重循环来遍历输出每一个元素：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
>>> for r in two_arr:  # row
...     for c in r:  # col
...         print(c)
...
0
1
2
3
4
5

# 如果你仅仅想查看数组中的元素，你可以先将多维数组平铺成一维数组，然后进行遍历查看：
>>> for item in two_arr.flatten():
...     print(item)
...
0
1
2
3
4
5

| ================================================== Split Line =============================================== |

👇👇👇 N 维数组 👇👇👇

推测一下 >>>> 单层 for 循环遍历多维数组时，会依次输出最高层次 axis 轴（axis=0）上的元素！！！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
>>> three_arr = np.arange(12).reshape(2, 2, 3)
>>> three_arr
array([[[ 0,  1,  2],
        [ 3,  4,  5]],

       [[ 6,  7,  8],
        [ 9, 10, 11]]])

>>> for item in three_arr:
...     print(item)
...
[[0 1 2]
 [3 4 5]]
[[ 6  7  8]
 [ 9 10 11]]

可以看出，对于高维数组（> 2-Dims）中元素的遍历访问是很繁琐的（多重 for 循环）。

迭代器方法

事实上，NumPy 中提供了一个 nditer 迭代器 方法 numpy.nditer()，可以配合 for 循环完成对数组中所有元素的遍历：

1
2
3
4
5
6
7
8
9
10
11
12
>>> arr = np.arange(12).reshape(2, 2, 3)
>>> arr
array([[[ 0,  1,  2],
        [ 3,  4,  5]],

       [[ 6,  7,  8],
        [ 9, 10, 11]]])

>>> for item in np.nditer(arr):
...     print(item, end=' ')
...
0 1 2 3 4 5 6 7 8 9 10 11

↓↓↓↓↓↓ 关于 C/F-Order ↓↓↓↓↓↓

我们知道，Ndarray 数组中元素有两种布局方式：C-order（行优先顺序）&& Fortrant-order（列优先顺序）。

那么，nditer 迭代器又是如何处理具有特定布局方式的数组呢？？？ >>>> 无须考虑布局（仅解释方式），Memory Block 中元素顺序遍历！！！

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
>>> arr = np.arange(6).reshape((2, 3), order="F")
>>> arr
array([[0, 2, 4],
       [1, 3, 5]])

# 和布局方式无关：
>>> for item in np.nditer(arr):
...     print(item, end=" ")
...
0 1 2 3 4 5

# 转置：
>>> for item in np.nditer(arr.T):
...     print(item, end=" ")
...
0 1 2 3 4 5

| ================================================== Split Line =============================================== |

👇👇👇 指定遍历顺序 👇👇👇

那么，如何通过指定的顺序（C/F-Order）访问 Ndarray 数组元素？？？可以通过 nditer 迭代器方法的 order 参数来指定：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
>>> arr = np.arange(6).reshape((2, 3))
>>> arr
array([[0, 1, 2],
       [3, 4, 5]])

# C-Order
>>> for item in np.nditer(arr, order='C'):
...     print(item, end=" ")
...
0 1 2 3 4 5

# F-Order
>>> for item in np.nditer(arr, order='F'):
...     print(item, end=" ")
...
0 3 1 4 2 5

| ================================================== Split Line =============================================== |

👇👇👇 遍历时修改元素值 👇👇👇

nditer 迭代器方法中提供有一个 op_flags 参数，可用于能否在遍历数组时对元素进行修改。有三种模式：

  • readonly：只读模式（默认），默认情况下不可更改；
  • readwrite：读写模式；
  • writeonly：只写模式。

实例代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
>>> arr = np.arange(6).reshape((2, 3))
>>> arr
array([[0, 1, 2],
       [3, 4, 5]])
>>> for item in np.nditer(arr):
...     item[...] = item * 2
...
# 默认情况下为 `read-only` 模式，不可修改：
Traceback (most recent call last):
  File "<stdin>", line 2, in <module>
ValueError: assignment destination is read-only

# 指定为可读写模式后，修改元素：
>>> for item in np.nditer(arr, op_flags=["readwrite"]):
...     item[...] = item * 2
...
>>> arr
array([[ 0,  2,  4],
       [ 6,  8, 10]])

| ================================================== Split Line =============================================== |

👇👇👇 同时迭代多数组 👇👇👇

如果多个数组之间可以被广播（Broadcast），那么 nditer 迭代器就可以同时对它们迭代。

关于数组的广播机制可参见下一章节~~~

实例代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
>>> a_arr = np.arange(6).reshape(2, 3)
>>> a_arr
array([[0, 1, 2],
       [3, 4, 5]])
>>> b_arr = np.arange(3)
>>> b_arr
array([0, 1, 2])

>>> for x,y in np.nditer([a_arr, b_arr]):
...     print ("%d-%d" % (x,y),end=",")
...
0-0,1-1,2-2,3-0,4-1,5-2

其中，数组 a_arr 的形状是 (2, 3)，而数组 b_arr 的形状是 (3,) <<<< 维度较小的数组 b_arr 可以被广播到数组 a_arr 中。

Ndarray Broadcast

当操作两个形状不同的数组运算时，会引发 NumPy 中的广播机制。

NumPy 中的广播机制（Broadcast）旨在 >>>> 解决 不同形状数组之间 的算术运算问题。

广播原则

这里，我们首先要了解广播机制的核心原则：

如果两个数组的后缘维度（Trailing Dimension，即从末尾开始算起的维度）的轴长度（相应轴上的元素个数，与 Shape 对应）相符，或其中至少一方的长度为 1，则认为它们是广播兼容的。

广播会在 >>>> 缺失和（或）长度为 1 的维度上对较小的数组进行扩展。

结合下面的广播应用理解其核心原则。

广播的应用

广播原则体现三种情况的应用：

  • 两个数组的维数不相等，但它们的后缘维度的轴长相符；
  • 两个数组的维数相等，但至少有一方轴的长度为 1；
  • 上述两种情况的结合。

👇👇👇 数组维度不同，后缘维度的轴长相符 👇👇👇

通过如下样例进行说明：

1
2
3
4
5
6
7
8
9
import numpy as np

>>> arr1 = np.array([[0, 0, 0],[1, 1, 1],[2, 2, 2], [3, 3, 3]])  #arr1.shape = (4, 3)
>>> arr2 = np.array([1, 2, 3])  # arr2.shape = (3,)
>>> print(arr1 + arr2)
[[1 2 3]
 [2 3 4]
 [3 4 5]
 [4 5 6]]

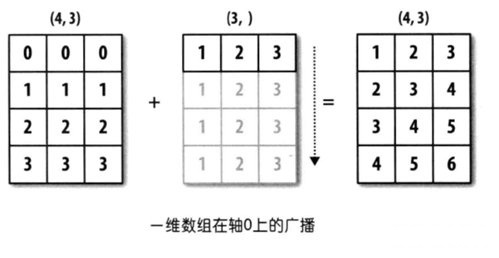
如上，Shape 不同的数组 arr1 和 arr2 可以通过广播原则执行加法运算。进一步解析 >>> 数组 arr1 && arr2 的维度不同：前者为二维的，而后者是一维的。但两个数组的后缘维度相等，会将较小的数组 arr2 沿着缺失的 0 轴进行扩展。

你可以认为 >>>> 较小数组的 shape，“截取” 自较大数组 shape 的尾部 <<<< 较小数组的 shape 刚好是某个后缘维度。

上述示例的广播示意图如下：

↓↓↓↓↓↓ 样例二 ↓↓↓↓↓↓

再来思考一下 arr3（3, 4, 2）&& arr4（4, 2）的情况 >>>> arr3 为 3 维，arr4 为 2 维，但其后缘维度相同（4, 2），axis=0 轴缺失。

其广播示意图如下：

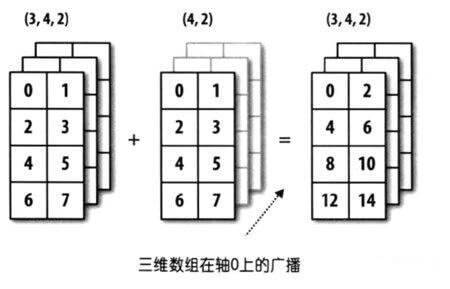
可见，对于较小的数组 arr4 将沿着缺失的 0 轴进行了扩展：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
>>> import numpy as np
>>> arr3 = np.arange(24).reshape([3, 4, 2])
>>> arr3
array([[[ 0,  1],
        [ 2,  3],
        [ 4,  5],
        [ 6,  7]],

       [[ 8,  9],
        [10, 11],
        [12, 13],
        [14, 15]],

       [[16, 17],
        [18, 19],
        [20, 21],
        [22, 23]]])
>>> arr4 = np.ones([4, 2])
>>> arr4
array([[1., 1.],
       [1., 1.],
       [1., 1.],
       [1., 1.]])
>>> print(arr3 + arr4)
[[[ 1.  2.]
  [ 3.  4.]
  [ 5.  6.]
  [ 7.  8.]]

 [[ 9. 10.]
  [11. 12.]
  [13. 14.]
  [15. 16.]]

 [[17. 18.]
  [19. 20.]
  [21. 22.]
  [23. 24.]]]

同理，（4, 2, 3）和（2, 3）是兼容的，（4, 2, 3）还和（3,）是兼容的，后者需要在两个轴上面进行扩展。

| ================================================== Split Line =============================================== |

👇👇👇 数组维度相同，其中至少有一个轴为 1 👇👇👇

通过如下样例进行说明：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
>>> import numpy as np
>>> arr1 = np.array([[0, 0, 0], [1, 1, 1], [2, 2, 2], [3, 3, 3]])
>>> arr1
array([[0, 0, 0],
       [1, 1, 1],
       [2, 2, 2],
       [3, 3, 3]])
>>> arr2 = np.array([[1], [2], [3], [4]])
>>> arr2
array([[1],
       [2],
       [3],
       [4]])

>>> print(arr1 + arr2)
[[1 1 1]
 [3 3 3]
 [5 5 5]
 [7 7 7]]

arr1 的 shape 为（4, 3），arr2 的 shape 为 （4, 1），它们都是二维的。并且，数组 arr2 在 axis=1 轴上的轴长度为 1，故其可以沿着该轴进行广播，其示意图如下：

当前情况下，两个数组的维度相同，较小数组的某个轴长度为 1，这样就会沿着长度为 1 的轴进行扩展。

同理，（4, 6）和（1, 6）是兼容的，（3, 5, 6）和（1, 5, 6）、（3, 1, 6）、（3, 5, 1）是兼容的，后面三个数组分别会沿着 0 轴，1 轴，2 轴进行广播。

| ================================================== Split Line =============================================== |

👇👇👇 上述两种情况的结合 👇👇👇

还有上面两种结合的情况：

如（3, 5, 6）和（1, 6）/（1, 1, 6）是可以相兼容的。

在 TensorFlow 当中计算张量的时候也是用广播机制，并且和 NumPy 的广播机制是一样的。

Ndarray 数组基本操作

NumPy 中包含了一些处理数组的常用方法，大致可分为以下几类：

  • 数组重塑操作；
  • 数组换轴操作；
  • 数组变维操作；
  • 数组扩展和压缩操作；
  • 数组连接与分割操作；
  • 数组的增删改查操作；
  • 数组的排序操作。

下面分别对它们进行介绍：

数组重塑

关于数组的简单变形操作涉及到几个常用函数：numpy.ndarray.reshape && numpy.ndarray.resize && numpy.ndarray.flat && numpy.ndarray.flatten && numpy.reval 等。

关于 numpy.ndarray.reshape 方法的用法，可参见上文关于【Ndarray 数组维度和形状】中说明，这里不再进行赘述。

↓↓↓↓↓↓ 1. numpy.ndarray.resize ↓↓↓↓↓↓

该函数可用于重塑 ndarray 数组的形状，其语法格式如下：

1
2
3
4
5
numpy.resize(array, newShape)

# 或：
# 同理于 NumPy 中 reshape 方法，但更加方便：
numpy.ndarray.resize(newShape)

实例如下：

1
2
3
4
5
6
7
8
9
>>> import numpy as np

>>> arr = np.arange(8)
>>> arr
array([0, 1, 2, 3, 4, 5, 6, 7])
>>> arr.resize(2, 4)
>>> arr
array([[0, 1, 2, 3],
       [4, 5, 6, 7]])

需要注意的是 >>> 修改 ndarray 数组形状（尺寸）的时候， 不能改变数组中元素的个数。如上面数组的形状是 8 * 1（8），可以修改成 2 * 4（8） && 4 * 2（8），修改后仍是 8 个。否则报错：

1
ValueError: cannot resize this array: it does not own its data

区别于 reshape 在于 是否影响原数组。reshape 在改变形状时，不会影响原数组，相当于对原数组做了一份拷贝；而 resize 则是对原数组执行操作。

| ================================================== Split Line =============================================== |

↓↓↓↓↓↓ 2. numpy.ndarray.flat ↓↓↓↓↓↓

类似于 numpy.nditer，该函数可用于返回一个数组迭代器（numpy.flatiter），可以配合 for 循环遍历数组中的每一个元素：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
>>> import numpy as np
>>> arr = np.arange(9).reshape(3, 3)
>>> for row in arr:
...     print(row)
...
[0 1 2]
[3 4 5]
[6 7 8]

>>> for ele in arr.flat:
...     print(ele, end=", ")
...
0, 1, 2, 3, 4, 5, 6, 7, 8,

>>> type(arr.flat)
<class 'numpy.flatiter'>

↓↓↓↓↓↓ 3. numpy.ndarray.flatten ↓↓↓↓↓↓

使数组扁平，该函数将以一维数组的形式（扁平处理）返回一份数组的副本（Copy），对副本的操作不会影响到原数组。

其语法格式如下：

1
numpy.ndarray.flatten(order='C')

实例代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
>>> import numpy as np
>>> arr = np.arange(9).reshape(3, 3)
>>> arr
array([[0, 1, 2],
       [3, 4, 5],
       [6, 7, 8]])

>>> flatten_of_arr = arr.flatten()
>>> flatten_of_arr
array([0, 1, 2, 3, 4, 5, 6, 7, 8])
# 数据所有者：
>>> flatten_of_arr.flags.owndata
True

# 行优先展开
>>> arr.flatten(order="F")
array([0, 3, 6, 1, 4, 7, 2, 5, 8])


| ================================================== Split Line =============================================== |

↓↓↓↓↓↓ 4. numpy.ndarray.ravel ↓↓↓↓↓↓

使数组扁平，该函数将以一维数组的形式（扁平处理）返回视图（View），如果修改会影响到原数组。

其语法格式如下：

1
numpy.ravel(order='C')

实例代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
>>> import numpy as np
>>> arr = np.arange(9).reshape(3, 3)
>>> arr
array([[0, 1, 2],
       [3, 4, 5],
       [6, 7, 8]])

>>> ravel_of_arr = arr.ravel()
>>> ravel_of_arr
array([0, 1, 2, 3, 4, 5, 6, 7, 8])
# 非数据所有者（引用）：
>>> ravel_of_arr.flags.owndata
False

# 列优先展开：
>>> arr.ravel(order="F")
array([0, 3, 6, 1, 4, 7, 2, 5, 8])

| ================================================== Split Line =============================================== |

↓↓↓↓↓↓ 5. numpy.fliplr && numpy.flipud ↓↓↓↓↓↓

NumPy 中还提供有直接对数组进行翻转的方法：

  • numpy.fliplr(arr)：左右翻转数组；
  • numpy.flipud(arr)：上下翻转数组。

实例代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
>>> import numpy as np
>>> arr = np.arange(16).reshape(4, 4)
>>> arr
array([[ 0,  1,  2,  3],
       [ 4,  5,  6,  7],
       [ 8,  9, 10, 11],
       [12, 13, 14, 15]])
>>> np.fliplr(arr)
array([[ 3,  2,  1,  0],
       [ 7,  6,  5,  4],
       [11, 10,  9,  8],
       [15, 14, 13, 12]])
>>> np.flipud(arr)
array([[12, 13, 14, 15],
       [ 8,  9, 10, 11],
       [ 4,  5,  6,  7],
       [ 0,  1,  2,  3]])

数组换轴

关于数组的换轴操作涉及到几个常用函数：numpy.moveaxis && numpy.swapaxes && numpy.transpose && numpy.ndarray.T 等。

↓↓↓↓↓↓ 1. numpy.moveaxis ↓↓↓↓↓↓

轴移动，该函数可用于将 Ndarray 数组的某个轴移动到特定位置，其语法格式如下：

1
numpy.moveaxis(arr, source, destination)

其中，参数 arr 表示某个数组，参数 source 表示要移动的轴的原始位置，参数 destination 表示要移动到的目标位置。

实例代码如下：

1
2
3
4
5
6
7
8
9
>>> import numpy as np
>>> x = np.zeros((3, 4, 5))

# 将 axis=0 移动到最后：
>>> np.moveaxis(x, 0, -1).shape
(4, 5, 3)
# 将 axis=2 移动到开始：
>>> np.moveaxis(x, -1, 0).shape
(5, 3, 4)

↓↓↓↓↓↓ 2. numpy.swapaxes ↓↓↓↓↓↓

轴交换，不同于 moveaxis 的是，该可以用于实现 Ndarray 数组轴的交换。其语法格式如下：

1
numpy.swapaxes(arr, axis1, axis2)

其中，参数 arr 表示某个数组，参数 axis1 表示需要交换的轴 1 的位置，参数 destination 表示需要交换的轴 2 的位置。

实例代码如下：

1
2
3
4
5
6
7
8
>>> import numpy as np
>>> x = np.zeros((3, 4, 5))

# 交换第一个和最后一个轴的位置：
>>> np.swapaxes(arr, 0, 2).shape
(5, 4, 3)
>>> np.swapaxes(arr, 0, -1).shape
(5, 4, 3)

| ================================================== Split Line =============================================== |

↓↓↓↓↓↓ 3. numpy.transpose ↓↓↓↓↓↓

轴调换，该函数可用于自由调换 Ndarray 数组的多个轴，其语法格式如下：

1
2
3
4
5
numpy.transpose(arr,  axes=None)

# 或：
# 同理于 NumPy 中 transpose 方法，但更加方便：
numpy.ndarray.transpose(*axes)

其中，参数 axes 表示调换后各轴顺序的元组或列表，当 axes=None（默认）时表示数组转置，等同于二维数组的 numpy.ndarray.T。

实例代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
>>> import numpy as np
>>> arr = np.arange(12).reshape(3, 4)
>>> arr
array([[ 0,  1,  2,  3],
       [ 4,  5,  6,  7],
       [ 8,  9, 10, 11]])

>>> arr.T
array([[ 0,  4,  8],
       [ 1,  5,  9],
       [ 2,  6, 10],
       [ 3,  7, 11]])

# 等同于 arr.T
>>> arr.transpose(1, 0)
array([[ 0,  4,  8],
       [ 1,  5,  9],
       [ 2,  6, 10],
       [ 3,  7, 11]])
>>> arr.transpose()
array([[ 0,  4,  8],
       [ 1,  5,  9],
       [ 2,  6, 10],
       [ 3,  7, 11]])

>>> three_arr = arr.reshape(3, 2, 2)
>>> three_arr
array([[[ 0,  1],
        [ 2,  3]],

       [[ 4,  5],
        [ 6,  7]],

       [[ 8,  9],
        [10, 11]]])
>>> three_arr.transpose(2, 0, 1)
array([[[ 0,  2],
        [ 4,  6],
        [ 8, 10]],

       [[ 1,  3],
        [ 5,  7],
        [ 9, 11]]])
>>> three_arr.transpose(2, 0, 1).shape
(2, 3, 2)

事实上，你可以非常灵活的实现数组的换轴操作：

1
2
3
4
5
6
7
8
9
10
11
>>> x = np.zeros((3, 4, 5))
>>> np.moveaxis(x, 0, -1).shape
(4, 5, 3)
>>> np.transpose(x).shape
(5, 4, 3)
>>> np.swapaxes(x, 0, -1).shape
(5, 4, 3)
>>> np.moveaxis(x, [0, 1], [-1, -2]).shape
(5, 4, 3)
>>> np.moveaxis(x, [0, 1, 2], [-1, -2, -3]).shape
(5, 4, 3)

关于数组换轴后，数组中数据排布情况，可参见 >>>【一文解析 NumPy ndarray 多维数组结构设计】博文中【Ndarray 属性详解】小节关于轴和形状的说明。

数组变维

NumPy 中还提供了形如 atleast_Xd 的函数，支持将输入数据的维度直接视为 X（1/2/3）维。其语法格式如下：

1
2
3
numpy.atleast_1d()
numpy.atleast_2d()
numpy.atleast_3d()

实例代码如下：

1
2
3
4
5
6
7
8
9
10
11
>>> np.atleast_1d([1, 2, 3])
array([1, 2, 3])
>>> np.atleast_2d([4, 5, 6])
array([[4, 5, 6]])
>>> np.atleast_2d([[1, 2, 3], [4, 5, 6]])
array([[1, 2, 3],
       [4, 5, 6]])
>>> np.atleast_3d([7, 8, 9])
array([[[7],
        [8],
        [9]]])

关于既有数组的变维操作，可以参见前文介绍过的 numpy.ndarray.reshape && numpy.ndarray.resize 函数。

数组扩展和压缩

关于数组的扩展和压缩操作涉及到几个常用函数：numpy.broadcast && numpy.broadcast_to && numpy.expand_dims && numpy.squeeze 等。

↓↓↓↓↓↓ 1. numpy.broadcast ↓↓↓↓↓↓

该函数用于生成一个模拟广播的对象（broadcast object），其返回一个广播对象，同样拥有 shape/ndim/size 等属性。

实例代码如下：

1
2
3
4
5
6
7
8
>>> import numpy as np
>>> a = np.array([[1], [2], [3]])
>>> b = np.array([4, 5, 6])

# 对 b 广播 a，这里数组的顺序，就是广播对象中相应数组的顺序（仅影响查看）
>>> d = np.broadcast(a, b)
>>> d
<numpy.broadcast object at 0x000001CFFA44B960>

既然是一个广播对象，我们无法直接查看其细节信息。广播对象提供了一个 iters 属性可用于迭代输出信息：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
>>> row, col = d.iters
# 查看广播对象中，相应行、列位置处，两个数组的元素情况：
>>> for idx in range(d.size):
...     print(next(row), next(col))
...
1 4
1 5
1 6
2 4
2 5
2 6
3 4
3 5
3 6

可见，对于数组 a 沿着轴为 1 的方向进行了扩展，而数组 b 沿着缺失的轴进行了扩展。

使用 broadcast 来完成 a+b 过程：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
# 先给出 a + b 的结果：
>>> a + b
array([[5, 6, 7],
       [6, 7, 8],
       [7, 8, 9]])

# 使用 broadcast 来完成 a + b：
>>> e = np.broadcast(a, b)
>>> f = np.empty(e.shape)
>>> f.flat = [x + y for (x, y) in e]
>>> f
array([[5., 6., 7.],
       [6., 7., 8.],
       [7., 8., 9.]])

↓↓↓↓↓↓ 2. numpy.broadcast_to ↓↓↓↓↓↓

很多时候，我们想要查看对于某个数组广播到某个 Shape 时的细节，怎么办？！！

NumPy 中提供了 numpy.broadcast_to 方法可以返回数组广播到新形状上的一个只读视图，其语法格式如下：

1
numpy.broadcast_to(array, shape)

实例代码如下：

1
2
3
4
5
6
7
8
9
# 查看上面实例中的数组 `a` && `b` 广播后的数组细节：
>>> np.broadcast_to(a, (3, 3))
array([[1, 1, 1],
       [2, 2, 2],
       [3, 3, 3]])
>>> np.broadcast_to(b, (3, 3))
array([[4, 5, 6],
       [4, 5, 6],
       [4, 5, 6]])

需要注意的是，如果新形状不符合 NumPy 的广播规则，则会抛出 ValueError 异常。

| ================================================== Split Line =============================================== |

↓↓↓↓↓↓ 3. numpy.expand_dims ↓↓↓↓↓↓

该函数可以在数组中指定轴位置插入新的轴，从而扩展数组的维度。其语法格式如下:

1
numpy.expand_dims(arr, axis)

其中，参数 axis 表示新轴插入的位置。

实例代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
>>> import numpy as np

>>> x = np.array(([1,2],[3,4]))
>>> x
array([[1, 2],
       [3, 4]])
>>> x.shape
(2, 2)

>>> y = np.expand_dims(x, axis=0)
>>> y
array([[[1, 2],
        [3, 4]]])
>>> y.shape
(1, 2, 2)

↓↓↓↓↓↓ 4. numpy.squeeze ↓↓↓↓↓↓

维度有扩展就有压缩，该函数可以删除数组中周长度为 1 的维度。例如，一个数组的 shape 是 (5, 1)，经此函数后，shape 变为 (5,) 。其函数语法格式如下：

1
numpy.squeeze(arr, axis)

其中，参数 axis 取值为整数或整数元组，用于指定需要删除的维度所在轴，其所指向的轴长必须为 1，否则会报错！！！若为 None，则删除数组中所有轴长为 1 的维度。

实例代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
>>> arr = np.array([[[0], [1], [2]]])
>>> arr.shape
(1, 3, 1)

# 删除所有：
>>> np.squeeze(arr).shape
(3,)
# 删除轴 `axis=0`
>>> np.squeeze(arr, axis=(0,)).shape
(3, 1)
# 删除轴 `axis=2`
>>> np.squeeze(arr, axis=(2,)).shape
(1, 3)

数组连接与拆分

关于数组的连接与分割操作涉及到几个常用函数：numpy.concatenate && numpy.stack && numpy.hstack && numpy.vstack numpy.dstack && numpy.column_stack() && numpy.split && numpy.hsplit && numpy.vsplit && numpy.dsplit 等。

👇👇👇 数组连接 👇👇👇

numpy.concatenate 函数可以将多个数组沿指定轴连接在一起。其语法格式如下：

1
numpy.concatenate((arr1, arr2, ...), axis=0)

其中，参数 (arr1, arr2, ...) 表示待连接的数组列表，参数 axis 表示指定的连接轴，默认为 0 轴。

实例代码如下：

1
2
3
4
5
6
7
8
9
10
11
>>> import numpy as np
>>> a = np.array([[1, 2], [3, 4], [5, 6]])
>>> b = np.array([[7, 8], [9, 10]])
>>> c = np.array([[11, 12]])
>>> np.concatenate((a, b, c), axis=0)
array([[ 1,  2],
       [ 3,  4],
       [ 5,  6],
       [ 7,  8],
       [ 9, 10],
       [11, 12]])

需要注意的是，需要保证连接处的维度一致！！！例如你可以尝试沿着横轴连接：

1
2
3
4
5
6
7
8
9
>>> import numpy as np
>>> a = np.array([[1, 2], [3, 4], [5, 6]])
>>> b = np.array([[7, 8, 9]])

# 为了保证连接处维度一致，需要对数组 b 进行转置
>>> np.concatenate((a, b.T), axis=1)
array([[1, 2, 7],
       [3, 4, 8],
       [5, 6, 9]])

👇👇👇 数组堆叠 👇👇👇

NumPy 中提供了以下方法，可用于数组的堆叠：

  • numpy.stack(arrays，axis)：沿着新轴连接数组的序列以实现堆叠；
  • numpy.column_stack()：将 1 维数组作为列堆叠到 2 维数组中；
  • numpy.hstack()：按水平方向堆叠数组；
  • numpy.vstack()：按垂直方向堆叠数组
  • numpy.dstack()：按深度方向堆叠数组。

下面分别来看其区别：

↓↓↓↓↓↓ 1. numpy.stack ↓↓↓↓↓↓

该函数会 创建一个新轴（新维度）来实现数组的堆叠。这里我们将通过一个样例来看数组的堆叠方法：

1
2
3
4
5
6
>>> import numpy as np

>>> a = np.arange(1, 7).reshape((2, 3))
>>> b = np.arange(7, 13).reshape((2, 3))
>>> c = np.arange(13, 19).reshape((2, 3))
>>> d = np.arange(19, 25).reshape((2, 3))

四个用于堆叠的数组如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
# 均为（2, 3）的二维数组：
>>> a
array([[1, 2, 3],
       [4, 5, 6]])
>>> b
array([[ 7,  8,  9],
       [10, 11, 12]])
>>> c
array([[13, 14, 15],
       [16, 17, 18]])
>>> d
array([[19, 20, 21],
       [22, 23, 24]])

接下来分别来看不同轴/维度上的堆叠实验：

[1] >>>> axis=0

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
>>> np.stack([a, b, c, d], axis=0)
array([[[ 1,  2,  3],
        [ 4,  5,  6]],

       [[ 7,  8,  9],
        [10, 11, 12]],

       [[13, 14, 15],
        [16, 17, 18]],

       [[19, 20, 21],
        [22, 23, 24]]])

>>> np.stack([a, b, c, d], axis=0).shape
(4, 2, 3)

形象理解 >>> axis 等于几就在哪个维度上进行堆叠。当 axis=0 时（会创建一个新轴），意味着每个数组都是一个整体，即（2, 3）的数组。故对于 0 维堆叠，相当于简单的数组罗列 <<< 比如四个数组分别表示 4 张图像矩阵，进行 0 维堆叠就是将它们按照顺序排放起来，形成一个（4, 2, 3）的三维数组。

[2] >>>> axis=1

1
2
3
4
5
6
7
8
9
10
11
12
13
>>> np.stack([a, b, c, d], axis=1)
array([[[ 1,  2,  3],
        [ 7,  8,  9],
        [13, 14, 15],
        [19, 20, 21]],

       [[ 4,  5,  6],
        [10, 11, 12],
        [16, 17, 18],
        [22, 23, 24]]])

>>> np.stack([a, b, c, d], axis=1).shape
(2, 4, 3)

形象理解 >>> axis 等于几就在哪个维度上进行堆叠。当 axis=1 时（会创建一个新轴），意味着第一个维度，即数组的每一行。故对于 1 维堆叠，会从 4 个（2, 3）的数组中，各自拿出自己的第一行元素进行堆叠形成 3 维数组的第一 “行”；各自拿出自己的第二行数据进行堆叠形成 3 维数组的第二 “行”，最终堆叠成一个（2, 4, 3）的三维数组。<<< 比如四个数组分别表示对同一张图像进行不同图像处理后的数组，进行 1 维堆叠可以这些不同处理方式的数据有条理的堆叠形成一个数组，方便后续的统一处理。

[3] >>>> axis=2

1
2
3
4
5
6
7
8
9
10
11
>>> np.stack([a, b, c, d], axis=2)
array([[[ 1,  7, 13, 19],
        [ 2,  8, 14, 20],
        [ 3,  9, 15, 21]],

       [[ 4, 10, 16, 22],
        [ 5, 11, 17, 23],
        [ 6, 12, 18, 24]]])

>>> np.stack([a, b, c, d], axis=2).shape
(2, 3, 4)

形象理解 >>> axis 等于几就在哪个维度上进行堆叠。当 axis=1 时（会创建一个新轴），意味着第二个维度，即数组的每一行中的更深一层的维度（单个元素）。注意这里不要理解为 2 维堆叠是对每一列拿出来进行堆叠！！！故对于 2 维堆叠，会从 4 个（2, 3）的数组中，各自拿出自己每个元素，在对应的位置，进行堆叠。<<< 比如四个数组分别一个图像的 R、G、B 数据（为了更加形象，图像应该是 3 个像素矩阵），进行 2 维堆叠后，不就构成了图像的 RGB 三通道的数组了嘛。

更形象的理解 >>> 对于三维立方体数组，进行 2 维堆叠后，之前每个数组都是三维立方体数组的一个竖截面~~~

显而易见的是，你可以发现数组堆叠（stack）和数组连接（concatenate）的区别 >>> 是否形成新的维度？！！

| ================================================== Split Line =============================================== |

↓↓↓↓↓↓ 2. numpy.hstack ↓↓↓↓↓↓

函数原型：hstack(tup) ，参数 tup 可以是元组，列表，或者 ndarray，其返回一个堆叠后的数组。从实例代码体会其含义：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
>>> import numpy as np
>>> a = [[1], [2], [3]]
>>> b = [[4], [5], [6]]
>>> np.hstack([a, b])
array([[1, 4],
       [2, 5],
       [3, 6]])

>>> c = np.arange(13, 19).reshape((2, 3))
>>> d = np.arange(19, 25).reshape((2, 3))
>>> np.hstack([c, d])
array([[13, 14, 15, 19, 20, 21],
       [16, 17, 18, 22, 23, 24]])

# 三维数组水平堆叠
>>> arr1 = np.arange(0, 8).reshape(2, 2, 2)
>>> arr2 = np.arange(8, 16).reshape(2, 2, 2)
>>> arr1
array([[[0, 1],
        [2, 3]],

       [[4, 5],
        [6, 7]]])
>>> arr2
array([[[ 8,  9],
        [10, 11]],

       [[12, 13],
        [14, 15]]])
>>> np.hstack((arr1, arr2))
array([[[ 0,  1],
        [ 2,  3],
        [ 8,  9],
        [10, 11]],

       [[ 4,  5],
        [ 6,  7],
        [12, 13],
        [14, 15]]])

可见，水平堆叠就是将数组沿【水平/横轴/列顺序】方向进行堆叠。

↓↓↓↓↓↓ 3. numpy.vstack ↓↓↓↓↓↓

函数原型：vstack(tup) ，参数 tup 可以是元组，列表，或者 ndarray，其返回一个堆叠后的数组。从实例代码体会其含义：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
>>> import numpy as np
>>> a = [[1], [2], [3]]
>>> b = [[4], [5], [6]]
>>> np.vstack((a, b))
array([[1],
       [2],
       [3],
       [4],
       [5],
       [6]])

>>> c = np.arange(13, 19).reshape((2, 3))
>>> d = np.arange(19, 25).reshape((2, 3))
>>> np.vstack((c, d))
array([[13, 14, 15],
       [16, 17, 18],
       [19, 20, 21],
       [22, 23, 24]])

# 三维数组垂直堆叠：
>>> np.vstack([arr1, arr2])
array([[[ 0,  1],
        [ 2,  3]],

       [[ 4,  5],
        [ 6,  7]],

       [[ 8,  9],
        [10, 11]],

       [[12, 13],
        [14, 15]]])

可见，垂直堆叠就是将数组按 垂直（行顺序）进行堆叠。

↓↓↓↓↓↓ 4. numpy.column_stack ↓↓↓↓↓↓

函数原型：column_stack(tup) ，参数 tup 可以是元组，列表，或者 ndarray，其返回一个堆叠后的数组。从实例代码体会其含义：

1
2
3
4
5
6
7
8
9
10
>>> import numpy as np
>>> a = np.arange(1, 7).reshape((2, 3))
>>> a
array([[1, 2, 3],
       [4, 5, 6]])
>>> e = [7, 8]

>>> np.column_stack((a, e))
array([[1, 2, 3, 7],
       [4, 5, 6, 8]])

可见，该函数会将一个 1 维数组作为列堆叠到 2 维数组中。

理解 >>> 数组堆叠是沿轴进行的，数组拆分是垂直于轴进行分割的！！！ <<< 可以帮助你加深数组堆叠和拆分的理解。

👇👇👇 数组拆分 👇👇👇

类似于数组堆叠（stack），NumPy 中也提供了以下方法，可用于数组的拆分：

  • numpy.split(arr，indices_or_sections，axis=0)：沿指定的轴将数组均匀分割为多个子数组；
  • numpy.hsplit(arr，indices_or_sections)：按水平方向将数组拆分成多个子数组；
  • numpy.vsplit(arr，indices_or_sections)：按垂直方向将数组拆分成多个子数组；
  • numpy.dsplit(arr，indices_or_sections)：按深度方向将数组拆分成多个子数组；
  • numpy.array_split(arr, indices_or_sections, axis=0)：沿指定的轴将数组近似均匀分割为多个子数组。

数组拆分之后返回的结果是一个列表（list），列表中的每一项元素均为一个子数组（array），类似于如下：

1
2
3
4
5
[array(...),
 array(...),
 array(...),
 array(...),
 ... ]

下面分别来看其区别：

↓↓↓↓↓↓ 1. numpy.split ↓↓↓↓↓↓

该函数，可以沿指定的轴将数组均匀分割为多个子数组。其语法格式如下：

1
numpy.split(arr，indices_or_sections，axis)

其中，参数 arr 表示待拆分的数组；参数 indices_or_sections >>> 如果是一个 1-D 数组，代表沿轴切分的位置（看作多个索引对，左开右闭）；如果是一个整数，表示平均切分的份数（必须均分，否则报错：ValueError: array split does not result in an equal division）。参数 axis 表示要沿着哪个轴进行切分，默认为 0，二维数组中表示横向切分，为 1 时表示纵向切分。

实例代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
>>> import numpy as np
>>> arr = np.arange(9)

# int >>> sections
>>> np.split(arr, 3)
[array([0, 1, 2]), array([3, 4, 5]), array([6, 7, 8])]

# 无法均分时会产生报错：
>>> np.split(arr, 4)
Traceback (most recent call last):
ValueError: array split does not result in an equal division

# 1-D array >>> indices (左开右闭)
>>> arr = np.arange(8)
>>> np.split(arr, [3, 5, 6, 10])
[array([0, 1, 2]), array([3, 4]), array([5]), array([6, 7]), array([], dtype=int32)]

常见机器学习用法 >>>> indices 为 (3,)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
>>> import numpy as np
>>> a = np.arange(8)
# 在第三、四列之间进行分隔：
>>> np.split(a, (3,))
[array([0, 1, 2]), array([3, 4, 5, 6, 7])]

# 机器学习中的用法说明：
# axis=1（代表列），是要把 data 数据集中的所有数据按第三、四列之间分割为 X 集和 Y 集。
x, y = np.split(data, (3,), axis=1)

# ↓↓↓↓↓↓ 样例 ↓↓↓↓↓↓
# 假设数组 arr 中每一行为一个样本数据（行中最后一个元素为样本对应的真实值）：
>>> arr = np.arange(20).reshape(4, 5)
>>> arr
array([[ 0,  1,  2,  3,  4],
       [ 5,  6,  7,  8,  9],
       [10, 11, 12, 13, 14],
       [15, 16, 17, 18, 19]])
# 划分出样本值 X 和真实值 Y 的数组：
>>> np.split(arr, (4,), axis=1)
[array([[ 0,  1,  2,  3],
       [ 5,  6,  7,  8],
       [10, 11, 12, 13],
       [15, 16, 17, 18]]), array([[ 4],
       [ 9],
       [14],
       [19]])]

| ================================================== Split Line =============================================== |

↓↓↓↓↓↓ 2. numpy.array_split ↓↓↓↓↓↓

不同于 numpy.split 的强制均匀分割，array_split 函数，可以沿指定的轴将数组 近似均匀分割 为多个子数组。其语法格式如下：

1
numpy.array_split(arr, indices_or_sections, axis=0)

数组近似拆分原则：前 L % n 个组的大小是（L // n + 1），剩下组的大小是（L // n）。其中 // 表示下取整（即 np.floor()），n 代表划分后数组的个数。

实例代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
>>> import numpy as np
>>> arr = np.arange(8)
# 默认垂直 axis=0 轴近似分割数组：
>>> np.array_split(arr, 3)
[array([0, 1, 2]), array([3, 4, 5]), array([6, 7])]

>>> arr1 = np.arange(14).reshape(2, 7)
>>> arr1
array([[ 0,  1,  2,  3,  4,  5,  6],
       [ 7,  8,  9, 10, 11, 12, 13]])
# 垂直 axis=1 轴近似分割数组：
>>> np.array_split(arr1, 2, axis=1)
[array([[ 0,  1,  2,  3],
       [ 7,  8,  9, 10]]), array([[ 4,  5,  6],
       [11, 12, 13]])]

| ================================================== Split Line =============================================== |

↓↓↓↓↓↓ 3. numpy.hsplit && numpy.vsplit ↓↓↓↓↓↓

垂直于 水平/竖直 轴拆分数组，要遵循均匀分割原则，否则报错。实例代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
# ↓↓↓↓↓↓ 水平分割 ↓↓↓↓↓↓ #
>>> a = [[1], [2], [3]]
>>> b = [[4], [5], [6]]
>>> res = np.hstack([a, b])
>>> res
array([[1, 4],
       [2, 5],
       [3, 6]])
# 拆分水平堆叠后的数组：
>>> np.hsplit(res, (1,))
[array([[1],
       [2],
       [3]]), array([[4],
       [5],
       [6]])]

>>> c = np.arange(13, 19).reshape((2, 3))
>>> d = np.arange(19, 25).reshape((2, 3))
>>> res = np.hstack([c, d])
>>> np.hsplit(res, (3,))
[array([[13, 14, 15],
       [16, 17, 18]]), array([[19, 20, 21],
       [22, 23, 24]])]

# ↓↓↓↓↓↓ 垂直分割 ↓↓↓↓↓↓ #
>>> a = [[1], [2], [3]]
>>> b = [[4], [5], [6]]
>>> res = np.vstack((a, b))
>>> res
array([[1],
       [2],
       [3],
       [4],
       [5],
       [6]])
# 拆分垂直堆叠后的数组：
>>> np.vsplit(res, (3,))
[array([[1],
       [2],
       [3]]), array([[4],
       [5],
       [6]])]

>>> c = np.arange(13, 19).reshape((2, 3))
>>> d = np.arange(19, 25).reshape((2, 3))
>>> res = np.vstack((c, d))
>>> res
array([[13, 14, 15],
       [16, 17, 18],
       [19, 20, 21],
       [22, 23, 24]])
>>> np.vsplit(res, (2,))
[array([[13, 14, 15],
       [16, 17, 18]]), array([[19, 20, 21],
       [22, 23, 24]])]

数组的增删改查

NumPy 中提供了对 Ndarray 数组中元素执行增、删、改、查等操作的方法，下面将分别介绍这些用法：

👇👇👇 数组删除 👇👇👇

↓↓↓↓↓↓ 1. numpy.delete ↓↓↓↓↓↓

numpy.delete 方法，可用于沿特定轴，删除数组中指定的子数组，返回一个新数组。其语法格式如下：

1
numpy.delete(arr, obj, axis)

其中，参数 obj 可以为整数、整数数组或切片，表示要被删除的数组元素或子数组。参数 axis 表示沿着哪条轴删除子数组，需要注意的是 >>> 若不提供 axis 参数，数组 arr 会先被展开为一维数组，然后进行删除。

实例代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
>>> import numpy as np
>>> arr = np.arange(12).reshape(3,4)
>>> arr
array([[ 0,  1,  2,  3],
       [ 4,  5,  6,  7],
       [ 8,  9, 10, 11]])

# 不提供 axis 参数情况下，删除了第 4 个元素（一维）：
>>> np.delete(arr, 3)
array([ 0,  1,  2,  4,  5,  6,  7,  8,  9, 10, 11])

# 删除第 3 列元素：
>>> np.delete(arr, 2, axis=1)
array([[ 0,  1,  3],
       [ 4,  5,  7],
       [ 8,  9, 11]])

# 删除经切片后的数组：
>>> arr_slice = np.delete(arr, np.s_[::2])
>>> arr_slice
array([ 1,  3,  5,  7,  9, 11])

↓↓↓↓↓↓ 2. numpy.unique ↓↓↓↓↓↓

该函数，可用于删除数组中重复的元素。其语法格式如下：

1
numpy.unique(arr, return_index=False, return_inverse=False, return_counts=False, axis=None)

其中，参数 return_index 为 True 时，返回新数组元素在原数组中的位置（索引）；参数 return_inverse 为 True 时，返回原数组元素在新数组中的位置（索引）；参数 return_counts 为 True 时，返回去重后的数组元素在原数组中出现的次数。

关于参数 axis=None（默认），会将多维数组平铺为一维，然后输出其中的重复元素。实例代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
>>> arr = np.array([5, 2, 6, 2, 7, 5, 6, 8, 2, 9])

# 默认去重：
>>> np.unique(arr)
array([2, 5, 6, 7, 8, 9])

# 新数组元素在原数组中的索引：
>>> u, indices = np.unique(arr, return_index=True)
>>> u
array([2, 5, 6, 7, 8, 9])
>>> indices
array([1, 0, 2, 4, 7, 9], dtype=int64)

# 原数组元素在新数组中的索引：
>>> u, indices = np.unique(arr, return_inverse=True)
>>> u
array([2, 5, 6, 7, 8, 9])
>>> indices
array([1, 0, 2, 0, 3, 1, 2, 4, 0, 5], dtype=int64)

# 新数组对应原数组中的元素重复次数：
>>> u, indices = np.unique(arr, return_counts=True)
>>> u
array([2, 5, 6, 7, 8, 9])
>>> indices
array([3, 2, 2, 1, 1, 1], dtype=int64)

而当 axis=0/1/2/... 时，会沿着相应的轴，删除轴上的重复元素（注意轴上的元素，并不是数组中的元素）：

1
2
3
4
>>> arr = np.array([[1, 0, 0], [1, 0, 0], [2, 3, 4], [1, 0, 0]])
>>> np.unique(arr, axis=0)
array([[1, 0, 0],
       [2, 3, 4]])

👇👇👇 数组增加 👇👇👇

关于增加数组元素，可分为插入和附加：

↓↓↓↓↓↓ 1. numpy.insert ↓↓↓↓↓↓

类似于 delete 用法，该函数可以沿指定的轴，在给定索引值的前一个位置进行插入（行前插入）。其语法格式如下：

1
numpy.insert(arr, obj, values, axis)

可以看到和 delete 的区别在于，需要在第三个参数位置设置需要插入的数组对象，并且 axis 用法同上。

实例代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
>>> import numpy as np
>>> arr = np.array([[1,2],[3,4],[5,6]])

# 不提供 axis 参数情况下，在第 3 个元素前插入（一维）：
>>> np.insert(arr, 2, [11,12])
array([ 1,  2, 11, 12,  3,  4,  5,  6])

# 沿轴 0 方向插入一行（广播原则）：
>>> np.insert(arr, 1, 11, axis = 0)
array([[ 1,  2],
       [11, 11],
       [ 3,  4],
       [ 5,  6]])
# 传入数组需要满足广播原则条件，否则报错：
>>> np.insert(arr, 1, [11, 12, 13], axis = 0)
Traceback (most recent call last):
ValueError: could not broadcast input array from shape (1,3) into shape (1,2)

# 沿轴 1 方向插入一列：
>>> np.insert(arr, 1, 11, axis = 1)
array([[ 1, 11,  2],
       [ 3, 11,  4],
       [ 5, 11,  6]])

↓↓↓↓↓↓ 2. numpy.append ↓↓↓↓↓↓

该函数可以沿指定的轴，在轴的末尾进行添加（不再需要位置参数）。其语法格式如下：

1
numpy.append(arr, values, axis=None)

其中，需要关注的参数是 axis，默认为 None，返回一个一维数组；对于二维数组，axis=0 追加的值会被添加到行，axis=1 恰好相反。

实例代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
>>> import numpy as np
>>> arr = np.array([[1,2,3],[4,5,6]])

# 默认 axis=None 的情况下：
>>> np.append(arr, [7,8,9])
array([1, 2, 3, 4, 5, 6, 7, 8, 9])

# 沿轴 0 方向，末尾添加一行：
>>> np.append(arr, [[7,8,9]], axis = 0)
array([[1, 2, 3],
       [4, 5, 6],
       [7, 8, 9]])

# 沿轴 1 方向，末尾添加三列
>>> np.append(arr, [[5,5,5],[7,8,9]], axis = 1)
array([[1, 2, 3, 5, 5, 5],
       [4, 5, 6, 7, 8, 9]])

需要注意的是 >>> 你需要保证添加轴上的维度一致！！！否则会产生报错。

👇👇👇 数组元素查询 👇👇👇

NumPy 中还提供了一些在数组内执行 搜索功能的 方法，以 了解数组内元素的细节情况。

这里比较简单，不进行赘述了。列举如下（使用时查表即可）：

  • numpy.nonzero(arr)：返回数组中非 0 元素的索引；
  • numpy.flatnonzero(arr)：平铺数组，并返回数组中非 0 元素的索引；
  • numpy.argmax(arr, axis, out)：返回数组中指定轴上的最大值的索引；
  • numpy.nanargmax(arr, axis)：返回数组中指定轴上的最大值的索引，忽略 NaN；
  • numpy.argmin(arr, axis, out)：返回数组中指定轴上的最小值的索引；
  • numpy.nanargmin(arr, axis)：返回数组中指定轴上的最小值的索引，忽略 NaN；
  • numpy.where(condition, [x, y])：根据指定条件，从指定行、列返回元素；
  • numpy.argwhere(arr)：返回数组中非 0 元素的索引，索引会按元素分组（表示一个非零元素）；
  • numpy.extract(condition, arr)：返回满足某些条件的数组的元素；
  • numpy.count_nonzero(arr, axis=None, keepdims=False)：统计数组中非 0 元素的数量。

实例代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
>>> import numpy as np

# ↓↓↓↓↓↓ 1. nonzero && flatnonzero && argwhere ↓↓↓↓↓↓ #
>>> x = np.array([[3, 0, 0], [0, 4, 0], [5, 6, 0]])
>>> x
array([[3, 0, 0],
       [0, 4, 0],
       [5, 6, 0]])
# 获取非零元素索引
>>> np.nonzero(x)
(array([0, 1, 2, 2]), array([0, 1, 0, 1]))
# 获取非零元素：
>>> x[np.nonzero(x)]
array([3, 4, 5, 6])
# 非零元素索引分组：
>>> np.transpose(np.nonzero(x))
array([[0, 0],
       [1, 1],
       [2, 0],
       [2, 1]])
# 分组返回非零元素索引
>>> np.argwhere(x)
array([[0, 0],
       [1, 1],
       [2, 0],
       [2, 1]], dtype=int64)
# 获取数组平铺后的非零元素索引
>>> np.flatnonzero(x)
array([0, 4, 6, 7], dtype=int64)
# 获取非零元素：
>>> x.ravel()[np.flatnonzero(x)]
array([3, 4, 5, 6])


# ↓↓↓↓↓↓ 2. argmin && nanargmin ↓↓↓↓↓↓ #
>>> x = np.array([[3,4,7], [8,2,1], [5,9,6]])
>>> x
array([[3, 4, 7],
       [8, 2, 1],
       [5, 9, 6]])
# 获取数组平铺后的最小元素索引
>>> np.argmin(x)
5
# 获取最小元素：
>>> x.ravel()[np.argmin(x)]
1
>>> np.argmin(x, axis=0)
array([0, 1, 1], dtype=int64)
>>> np.argmin(x, axis=1)
array([0, 2, 0], dtype=int64)


# ↓↓↓↓↓↓ 3. argmax && nanargmax ↓↓↓↓↓↓ #
>>> x = np.array([[3,4,7], [8,2,1], [5,9,6]])
>>> x
array([[3, 4, 7],
       [8, 2, 1],
       [5, 9, 6]])
# 获取数组平铺后的最大元素索引
>>> np.argmax(x)
7
# 获取最大元素：
>>> x.ravel()[np.argmax(x)]
9
>>> np.argmax(x, axis=0)
array([1, 2, 0], dtype=int64)
>>> np.argmax(x, axis=1)
array([2, 0, 1], dtype=int64)


# ↓↓↓↓↓↓ 4. where ↓↓↓↓↓↓ #
# An array with elements from `x` where `condition` is True,
# and elements from `y` elsewhere.
>>> a = np.arange(8).reshape(2, 4)
>>> a
array([[0, 1, 2, 3],
       [4, 5, 6, 7]])
>>> np.where(a<5, a, a*5)
array([[ 0,  1,  2,  3],
       [ 4, 25, 30, 35]])
# 默认情况下，返回满足条件的索引值：
>>> a = np.arange(8, 16).reshape(2, 4)
>>> a
array([[ 8,  9, 10, 11],
       [12, 13, 14, 15]])
>>> np.where(a>10)
(array([0, 1, 1, 1, 1], dtype=int64), array([3, 0, 1, 2, 3], dtype=int64))
>>> a[np.where(a>10)]
array([11, 12, 13, 14, 15])


# ↓↓↓↓↓↓ 5. extract ↓↓↓↓↓↓ #
>>> arr = np.arange(12).reshape((3, 4))
>>> arr
array([[ 0,  1,  2,  3],
       [ 4,  5,  6,  7],
       [ 8,  9, 10, 11]])
>>> condition = np.mod(arr, 3)==0
>>> condition
array([[ True, False, False,  True],
       [False, False,  True, False],
       [False,  True, False, False]])
# 返回数组中使得条件为 True 的元素的值：
>>> np.extract(condition, arr)
array([0, 3, 6, 9])


# ↓↓↓↓↓↓ 6. count_nonzero ↓↓↓↓↓↓ #
>>> a = np.array([[0, 1, 7, 0],
...               [3, 0, 2, 19]])
>>> np.count_nonzero(a)
5
# 沿着轴 0 统计非零元素数目：
>>> np.count_nonzero(a, axis=0)
array([1, 1, 2, 1])
# 沿着轴 1 统计非零元素数目：
>>> np.count_nonzero(a, axis=1)
array([2, 3])
# 统计时，保留数组维度信息：
>>> np.count_nonzero(a, axis=1, keepdims=True)
array([[2],
       [3]], dtype=int64)

数组的排序

NumPy 中还提供了一个对数组内元素进行排序的方法，返回一个数组副本（Copy）。其语法格式如下：

1
numpy.sort(arr, axis=-1, kind='quicksort', order=None)

其中，参数 axis 表示要排序的轴，默认 -1 表示沿最后一个轴进行排序；如果为 None，表示排序前要将数组铺平。参数 kind 表示要采用的排序算法，有三种模式 {‘quicksort’（快速排序），’mergesort’（归并排序），’heapsort’（堆排序）}。参数 order 表示，如果数组设置了字段，则 order 表示要排序的字段。

实例代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
>>> import numpy as np

>>> arr = np.array([[3,7],[9,1]])
>>> arr
array([[3, 7],
       [9, 1]])
# 默认情况下，沿着最后的轴（axis=1）进行排序：
>>> np.sort(arr)
array([[3, 7],
       [1, 9]])
# 沿着轴 0 进行排序：
>>> np.sort(arr, axis = 0)
array([[3, 1],
       [9, 7]])

# 若数组设置了 `name` && `age` 字段：
>>> dt = np.dtype([('name',  'S10'),('age',  int)])
>>> arr = np.array([("raju", 21),("anil", 25),("ravi", 17),  ("amar", 27)], dtype = dt)
>>> arr
array([(b'raju', 21), (b'anil', 25), (b'ravi', 17), (b'amar', 27)],
      dtype=[('name', 'S10'), ('age', '<i4')])
# 按照年龄字段进行排序：
>>> np.sort(arr, order = 'age')
array([(b'ravi', 17), (b'raju', 21), (b'anil', 25), (b'amar', 27)],
      dtype=[('name', 'S10'), ('age', '<i4')])

其它排序方法 >>>

  • numpy.argsort(arr , axis=-1, kind=None, order=None)：沿指定的轴，对数组的元素值进行排序，返回排序后的元素 索引数组；
  • numpy.lexsort(keys, axis)：按 键序列 对数组进行排序，返回一个已排序的 索引数组。

实例代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
>>> import numpy as np

>>> arr = np.array([90, 29, 89, 12])
# 获取排序后数组元素索引数组：
>>> np.argsort(arr)
array([3, 1, 2, 0], dtype=int64)
# 排序后数组：
>>> arr[np.argsort(arr)]
array([12, 29, 89, 90])

>>> a = [1,5,1,4,3,4,4] # First column
>>> b = [9,4,0,4,0,2,1] # Second column
>>> ind = np.lexsort((b,a)) # Sort by a, then by b
>>> ind
array([2, 0, 4, 6, 5, 3, 1])

>>> [(a[i],b[i]) for i in ind]
[(1, 0), (1, 9), (3, 0), (4, 1), (4, 2), (4, 4), (5, 4)]

NumPy 随机数

NumPy 中还提供了一个随机功能模块（numpy.random），以提供随机数功能。基本的随机函数如下：

↓↓↓↓↓↓ 1. numpy.random.rand ↓↓↓↓↓↓

该方法用于，指定一个给定维度的数组（(d0, d1, ..., dn)），并使用 [0, 1) 区间随机数据填充，数据均匀分布。其语法格式如下：

1
numpy.random.rand(d0, d1, ..., dn)

实例代码如下：

1
2
3
4
5
6
7
>>> import numpy as np

# 生成一个元素值区间在 `[0, 1)` 的二维的，形状为（3, 2）的数据均匀分布的数组： 
>>> np.random.rand(3, 2)
array([[0.9766812 , 0.38515738],
       [0.59869254, 0.26848813],
       [0.98355621, 0.51861994]])

↓↓↓↓↓↓ 2. numpy.random.randn ↓↓↓↓↓↓

不同于 numpy.random.rand 的，该函数会生成一个元素值满足标准正态分布的数组。其语法格式同 rand：

1
numpy.random.randn(d0, d1, ..., dn)

实例代码如下：

1
2
3
4
5
6
7
8
9
10
>>> import numpy as np
# 生成一个元素值满足标准正态分布的，其形状为（2, 4）的二维数组:
>>> np.random.randn(2, 4)
array([[ 0.28689859,  0.62225787, -0.74514634, -1.28207413],
       [ 0.08684388,  0.4530653 , -1.61979964, -1.17046996]])

# 你还可以：
>>> 1 + 2.5 * np.random.randn(2, 4)
array([[ 0.04701047, -1.93698022,  0.2829873 ,  1.74470424],
       [ 0.37269291,  1.13634982,  0.05891712, -0.78763252]])

| ================================================== Split Line =============================================== |

↓↓↓↓↓↓ 3. numpy.random.randint ↓↓↓↓↓↓

该函数会生成一个元素值位于特定区间的，随机整数数组。其语法格式如下：

1
numpy.random.randint(low, high=None, size=None, dtype=int)

其中，前两个参数表示区间的上下限 [low, high) <<< 前闭后开的；参数 size 用来指定数组尺寸。

实例代码如下：

1
2
3
4
5
>>> import numpy as np

>>> np.random.randint(5, 10, size=(2, 4))
array([[7, 7, 7, 8],
       [6, 6, 6, 8]])

↓↓↓↓↓↓ 4. numpy.random.random_sample ↓↓↓↓↓↓

该函数会生成一个元素值位于 [0, 1) 的，指定大小（size）的，随机浮点数数组。其语法格式如下：

1
numpy.random.random_sample(size=None)

实例代码如下：

1
2
3
4
5
6
7
8
9
10
11
>>> import numpy as np

>>> np.random.random_sample()
0.9886997552147712
# 生成一个一维数组：
>>> np.random.random_sample((5,))
array([0.70472921, 0.63700827, 0.58702326, 0.95931205, 0.25185975])
# 生成一个形状为（2, 4）的二维数组：
>>> np.random.random_sample((2, 4))
array([[0.50799584, 0.92990624, 0.8807129 , 0.20741762],
       [0.93899597, 0.74072453, 0.60292363, 0.50895451]])

还有三个类似于 numpy.random.random_sample 的方法，如下：

  • numpy.random.random([size])
  • numpy.random.sample([size])
  • numpy.random.ranf([size])

| ================================================== Split Line =============================================== |

↓↓↓↓↓↓ 5. numpy.random.choice ↓↓↓↓↓↓

随机抽样生成 >>> 该函数会 从给定的数组里随机抽取几个值，生成指定大小（size）的，随机抽样数组。其语法格式如下：

1
numpy.random.choice(arr, size=None, replace=True, p=None)

其中，参数 arr 表示给定的或随机抽样的数组或整数，整数时同理于 np.arange(arr)；参数 replace 表示数组中的元素是否可以多次重复抽样；参数 p 用于指定数组元素关联的概率，不设定的话表示数组 arr 中元素均匀分布。

实例代码如下：

1
2
3
4
5
6
7
8
9
10
>>> import numpy as np

# np.arange(5) 中 3 出现的概率为 0.6：
>>> np.random.choice(5, 3, p=[0.1, 0, 0.3, 0.6, 0])
array([3, 3, 0]) # random

>>> aa_milne_arr = ['pooh', 'rabbit', 'piglet', 'Christopher']
>>> np.random.choice(aa_milne_arr, 5, p=[0.5, 0.1, 0.1, 0.3])
array(['pooh', 'pooh', 'pooh', 'Christopher', 'piglet'], # random
       dtype='<U11')

👇👇👇 概率密度分布 👇👇👇

NumPy 还提供了大量的满足特定概率密度分布的样本生成方法，使用和上述方法类似，使用时查表即可。如下：

  • numpy.random.beta(a，b，size)：从 Beta 分布中生成随机数；
  • numpy.random.binomial(n, p, size)：从二项分布中生成随机数；
  • numpy.random.chisquare(df，size)：从卡方分布中生成随机数；
  • numpy.random.dirichlet(alpha，size)：从 Dirichlet 分布中生成随机数；
  • numpy.random.exponential(scale，size)：从指数分布中生成随机数；
  • numpy.random.f(dfnum，dfden，size)：从 F 分布中生成随机数；
  • numpy.random.gamma(shape，scale，size)：从 Gamma 分布中生成随机数；
  • numpy.random.geometric(p，size)：从几何分布中生成随机数；
  • numpy.random.gumbel(loc，scale，size)：从 Gumbel 分布中生成随机数；
  • numpy.random.hypergeometric(ngood, nbad, nsample, size)：从超几何分布中生成随机数；
  • numpy.random.laplace(loc，scale，size)：从拉普拉斯双指数分布中生成随机数；
  • numpy.random.logistic(loc，scale，size)：从逻辑分布中生成随机数；
  • numpy.random.lognormal(mean，sigma，size)：从对数正态分布中生成随机数；
  • numpy.random.logseries(p，size)：从对数系列分布中生成随机数；
  • numpy.random.multinomial(n，pvals，size)：从多项分布中生成随机数；
  • numpy.random.multivariate_normal(mean, cov, size)：从多变量正态分布绘制随机样本；
  • numpy.random.negative_binomial(n, p, size)：从负二项分布中生成随机数；
  • numpy.random.noncentral_chisquare(df，nonc，size)：从非中心卡方分布中生成随机数；
  • numpy.random.noncentral_f(dfnum, dfden, nonc, size)：从非中心 F 分布中抽取样本；
  • numpy.random.normal(loc，scale，size)：从正态分布绘制随机样本；
  • numpy.random.pareto(a，size)：从具有指定形状的 Pareto II 或 Lomax 分布中生成随机数；
  • numpy.random.poisson(lam，size)：从泊松分布中生成随机数；
  • numpy.random.power(a，size)：从具有正指数 a-1 的功率分布中在 0，1 中生成随机数；
  • numpy.random.rayleigh(scale，size)：从瑞利分布中生成随机数；
  • numpy.random.standard_cauchy(size)：从标准 Cauchy 分布中生成随机数；
  • numpy.random.standard_exponential(size)：从标准指数分布中生成随机数；
  • numpy.random.standard_gamma(shape，size)：从标准 Gamma 分布中生成随机数；
  • numpy.random.standard_normal(size)：从标准正态分布中生成随机数；
  • numpy.random.standard_t(df，size)：从具有 df 自由度的标准学生 t 分布中生成随机数；
  • numpy.random.triangular(left，mode，right，size)：从三角分布中生成随机数；
  • numpy.random.uniform(low，high，size)：从均匀分布中生成随机数；
  • numpy.random.vonmises(mu，kappa，size)：从 Von Mises 分布中生成随机数；
  • numpy.random.random.wald(mean，scale，size)：从 Wald 或反高斯分布中生成随机数；
  • numpy.random.weibull(a，size)：从威布尔分布中生成随机数；
  • numpy.random.zipf(a，size)：从 Zipf 分布中生成随机数。

NumPy 数学函数

Python 自带的运算符只能完成一些基本的数组运算，对于更加复杂的数学计算就显得捉襟见肘。

显而易见的，NumPy 为我们提供了更多的数学函数，以帮助我们更好地完成复杂的数值计算！！！

Numpy 代数支持

参考链接：

https://blog.csdn.net/a1097304791/article/details/120901716
https://www.runoob.com/numpy/numpy-ndarray-object.html
http://c.biancheng.net/
https://blog.csdn.net/weixin_44330492/article/details/100126774
https://blog.csdn.net/csdn15698845876/article/details/73380803

Python 数据分析之 NumPy 数学计算库

https://www.orangeshare.cn/2018/01/20/python-shu-ju-fen-xi-zhi-numpy-shu-xue-ji-suan-ku/

Author

Waldeinsamkeit

Posted on

2018-01-20

Updated on

2023-05-09

Licensed under

#
You need to set install_url to use ShareThis. Please set it in _config.yml.

Like this article? Support the author with

Comments

You forgot to set the shortname for Disqus. Please set it in _config.yml.
×