一文解析 NumPy ndarray 多维数组结构设计

从 NumPy ndarray 的内存布局以及设计哲学，深入浅析 ndarray 多维数组的结构设计，以及相关属性。

What is NumPy?

官方描述 >>>

NumPy provides an N-dimensional array type, the ndarray, which describes a collection of “items” of the same type. The items can be indexed using for example N integers.

ndarray 是 NumPy 中的 多维数组，由 数据类型相同 的元素组成的元素序列，且可以被 索引。

如下所示：

>>> import numpy as np

# 定义一个三维数组：
>>> arr = np.array([[[0, 1, 2], [3, 4, 5]], [[6, 7, 8], [9, 10 ,11]]])
>>> arr
array([[[ 0,  1,  2],
        [ 3,  4,  5]],

       [[ 6,  7,  8],
        [ 9, 10, 11]]])
>>> type(arr)
<class 'numpy.ndarray'>

# 数组元素类型：
>>> arr.dtype
dtype('int32')

# 数组维度：
>>> arr.ndim
3
# 数组形状：
>>> arr.shape
(2, 2, 3)
# 数组维间距（步幅）：
>>> arr.strides
(24, 12, 4)

# 索引：
>>> arr[0, 1, 1]
4
>>> arr[0, 0]
array([0, 1, 2])

NumPy 数值计算库的核心特性 >>> 定义了一个 n 维数组对象，ndarray 对象（NumPy 数组也就是 ndarray 多维数组），拥有丰富的数学函数，以及对高维数组的直接处理能力。

---

Ndarray 的内存布局

首先给出 ndarray 的内存布局示意图：

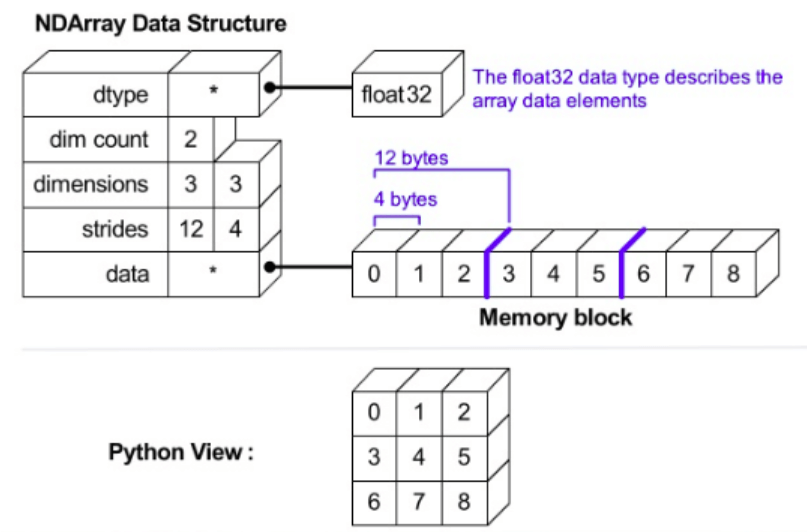
可大致划分成 2 部分 >>>数据部分和解释方式：

1. raw array data ：为一个连续的 Memory Block，存储着原始数据，以类似 C 或 Fortran 中的数组进行连续存储；
2. metadata ：对上面内存块的解释方式。

其中，metadata 包含如下信息：

• dtype：数据类型 >>> 指定了数组中每个元素占用多少个字节，这几个字节怎么解释（例如：int32、float32 等 NumPy 数据类型）；
• ndim（dim count）：数组维度（数值） >>> 数组有多少维；
• shape（dimensions）：数组形状（元组） >>> 每个维度上的元素数量；
• strides：维间距或步幅（元组） >>> 到达当前维下一个相邻数据需要前进的字节数；

以上 4 个信息构成了 ndarray 的 indexing schema >>> 如何索引到指定位置的数据，以及这个数据该怎么解释。

除此之外的信息还有：字节序（大端小端）、读写权限、C-order（行优先存储） or Fortran-order（列优先存储）等，如下所示:

>>> arr.flags
  C_CONTIGUOUS : True
  F_CONTIGUOUS : False
  OWNDATA : True
  WRITEABLE : True
  ALIGNED : True
  WRITEBACKIFCOPY : False
  UPDATEIFCOPY : False

可以很清晰看出，Ndarray 内存设计 >>> 将数组的 数据部分 && 解释方式 进行了分离。

---

Ndarray 的设计哲学

事实上， Ndarray 数组的设计哲学就在于 数据存储 && 与其解释方式 的分离，或者说 >>> 副本（copy） && 视图（view） 分离。这种分离方式，让尽可能多的操作发生在 解释方式（view）上，而尽量少地操作实际存储数据的内存区域。

简单来说，副本和视图是使用原数组的两种不同方式。先来看一个样例：

>>> import numpy as np
>>> arr = np.arange(4)

>>> print(arr)
[0 1 2 3]
# 整数数组索引：
>>> print(arr[[1, 2]])
[1 2]
# 切片（Slice）
>>> print(arr[1:3])
[1 2]


# base 属性：
>>> print(arr.base)
None
>>> print(arr[[1, 2]].base)
None
>>> print(arr[1:3].base)
[0 1 2 3]


# flags.owndata 属性：
>>> print(arr.flags.owndata)
True
>>> print(arr[[1, 2]].flags.owndata)
True
>>> print(arr[1:3].flags.owndata)
False

样例分析：虽然 a[[1, 2]] 和 a[1:3] 的输出结果相同，但从 base && flags.owndata 属性的输出结果来看，两者是有差别的。这是因为，a[[1, 2]] 得到的是原数组的副本（copy），而 a[1:3] 得到的是原数组的视图（view）。

那么 base && flags.owndata 属性到底代表数组的什么？！！

| ==================================== 👇👇👇 base && flags.owndata 👇👇👇 ==================================== |

我们提到过，Numpy 数组的内部结构包括：数据部分（数据存储区）&& 解释方式（数据结构信息区）。

数据存储区是用于存储数组的数据 >>> Numpy 数组中的数据可以指向其它数组中的数据，这样多个数组可以共用同一个数据（数据共享）。

• ndarray.base：用于判断数组中的数据是否来自于别的数组；
• ndarray.flags.owndata：用于判断数组是否是数据的所有者；

就上例而言，arr.base 和 arr[[1, 2]].base 返回的都是 None，说明两个数组中的数据均来自于自生。而 arr.flags.owndata 和 arr[[1, 2]].flags.owndata 返回的都是 True，说明两个数组都是数据的所有者。

我们再使用 ndarray.ctypes.data 属性来查看一下数组中数据（Memory Block）的物理地址验证一下：

>>> arr.ctypes.data
2302028351600
# 原始数组 arr 中数据 Memory Block 的物理地址范围：
>>> print('data buff address from {0} to {1}'.format(arr.ctypes.data, arr.ctypes.data + arr.nbytes))
data buff address from 2302028351600 to 2302028351616

# 仍位于 arr 的数据块中，共享数据，是原数组的视图（view）
>>> arr[1:3].ctypes.data
2302028351604

# 已不在 arr 的数据块中，拥有自己的数据块，是原数组的副本（copy）
>>> arr[[1, 2]].ctypes.data
2302028205472

| ================================================== Split Line =============================================== |

重新来看：a[[1, 2]] 得到的是原数组的副本（copy），而 a[1:3] 得到的是原数组的视图（view）？

• 视图是对原数组的引用，或者自身没有数据，与原数组共享数据；
• 副本是对原数组的完整拷贝，虽然由原数组中数据拷贝而来，但是它相对于原数组是独立的；

---

视图（View）

NumPy 中满足如下可产生原数组的视图（View）：

• 对原数组的引用；
• 自身没有数据，与原数组共享数据；

如下所示：

>>> import numpy as np
>>> arr = np.arange(12)
>>> arr
array([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11])


### =========== 1. 赋值引用 =========== ###
>>> cite_of_arr = arr
>>> cite_of_arr
array([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11])

# 内存地址相同（id），为同一数组，只是一个别名：
>>> id(arr)
1910433736304
>>> id(cite_of_arr)
1910433736304
# 既然是同一个数组，故：
>>> print(arr.base)
None
>>> print(cite_of_arr.base)
None
>>> print(arr.flags.owndata)
True
>>> print(cite_of_arr.flags.owndata)
True
### ================================= ###

### =========== 2. view() 函数 =========== ###
>>> view_of_arr = arr.view()
>>> view_of_arr.shape = (3, 4)
>>> view_of_arr
array([[ 0,  1,  2,  3],
       [ 4,  5,  6,  7],
       [ 8,  9, 10, 11]])

>>> print(arr.base)
None
# view_of_arr 数组不是其数据的所有者，数据共享于 arr：
>>> print(view_of_arr.base)
[ 0  1  2  3  4  5  6  7  8  9 10 11]
>>> print(arr.flags.owndata)
True
>>> print(view_of_arr.flags.owndata)
False

# ndarray.view() 操作产生的是 view 视图，只是对数据的解释方式发生变化（形状变化），数据物理地址相同：
>>> arr.ctypes.data
1910429914608
>>> view_of_arr.ctypes.data
1910429914608
### ===================================== ###

### =========== 3. reshape 操作 =========== ###
>>> reshape_of_arr = arr.reshape(4, 3)
>>> reshape_of_arr
array([[ 0,  1,  2],
       [ 3,  4,  5],
       [ 6,  7,  8],
       [ 9, 10, 11]])

>>> print(arr.base)
None
# reshape_of_arr 数组不是其数据的所有者，数据共享于 arr：
>>> print(reshape_of_arr.base)
[ 0  1  2  3  4  5  6  7  8  9 10 11]
>>> print(arr.flags.owndata)
True
>>> print(reshape_of_arr.flags.owndata)
False

# reshape 操作产生的是 view 视图，只是对数据的解释方式发生变化（形状变化），数据物理地址相同：
>>> arr.ctypes.data
1910429914608
>>> reshape_of_arr.ctypes.data
1910429914608
### ======================================= ###

### =========== 4. ndarray.T 转置操作 =========== ###
>>> transpose_of_arr = reshape_of_arr.T
>>> transpose_of_arr
array([[ 0,  3,  6,  9],
       [ 1,  4,  7, 10],
       [ 2,  5,  8, 11]])

# reshape_of_arr 数组不是其数据的所有者，数据共享于 arr：
>>> print(transpose_of_arr.base)
[ 0  1  2  3  4  5  6  7  8  9 10 11]
>>> print(transpose_of_arr.flags.owndata)
False

# Transpose 转置操作产生的是 view 视图，只是对数据的解释方式发生变化（形状变化），数据物理地址相同：
>>> transpose_of_arr.ctypes.data
1910429914608

视图原理剖析示意图 >>>

可见，view() 函数 && reshape 操作 && transpose && Slice 操作生成的是原数组视图（view），共用原数组 arr 数据存储区中的数据，但由于它们都有属于自己的数据结构信息区，因此可以将 arr 数组中的原始数据以自己的方式进行表达（指定不同的形状、dtype 等）。

view 机制的好处显而易见，省内存，同时速度快~~~

---

副本（Copy）

副本是对原数组的完整拷贝，虽然由原数组中数据拷贝而来，但是它相对于原数组是独立的。

使用 copy() 函数 && 数组高级索引方法，均可以返回数组的副本（Copy）。

如下所示：

>>> import numpy as np
>>> arr = np.arange(12)
>>> arr
array([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11])

# copy 函数生成副本：
>>> copy_of_arr = arr.copy()
>>> copy_of_arr
array([ 0,  1,  2,  3,  4,  5,  6,  7,  8,  9, 10, 11])

# # copy_of_arr 数组是其数据的所有者，拷贝但独立于 arr：
>>> print(arr.base)
None
>>> print(copy_of_arr.base)
None
>>> print(arr.flags.owndata)
True
>>> print(copy_of_arr.flags.owndata)
True

# 
>>> arr.ctypes.data
1910429914608
# 原始数组 arr 中数据 Memory Block 的物理地址范围：
>>> print('data buff address from {0} to {1}'.format(arr.ctypes.data, arr.ctypes.data + arr.nbytes))
data buff address from 1910429914608 to 1910429914656

# 可见，ndarray.copy() 操作产生的是 copy 副本，数据物理地址不相同：
>>> copy_of_arr.ctypes.data
1910429916208

副本图原理剖析示意图 >>>

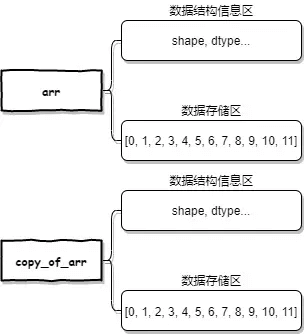
由于副本和原数组是相互独立的，改变副本或者原数组中的元素值，相对应的原数组和副本中的元素值并不会发生改变！！！

---

设计的优异性

为什么 ndarray 可以这样设计？！！

由于 ndarray 是为数组和矩阵运算服务的，ndarray 数组中的所有数据都是同一种类型（设计核心依据）（如 int32 && float64...），其稠密地排列在一起（元素序列）。取出时根据 dtype 现 copy 一份数据组装成 scalar 对象输出。

这样极大地节省了空间，scalar对象中除了数据之外的域没必要重复存储，同时因为连续内存的原因，可以按秩访问，速度也要快得多。

👇👇👇 Ndarray 性能优势 👇👇👇

这里，可以将 ndarray 与 Python 中的 list 对比一下 >>>>

List 可以容纳不同类型的对象，像 string、int、tuple 等都可以放在一个 List 里。故 List 中存放的是对象的引用，再通过引用找到具体的对象，这些对象所在的物理地址并不是连续的，如下所示：

所以相对 ndarray >>>

• List 访问到数据需要多跳转 1 次，List 只能做到对对象引用的按秩访问，对具体的数据并不是按秩访问，所以效率上 ndarray 比 List 要快得多；
• 空间上，ndarray 只把数据紧密存储，而 List 需要把每个对象的所有域值都存下来，所以 ndarray 比 List 要更省空间。

ndarray 设计机制的好处显而易见，省内存，同时速度快~~~

---

N-Darray 的理解

如何合理的想象多维数组？？？

以图书馆来举例：

一维数组 >>> 一条线（一个行/列向量）

二维数组 >>> 一页纸

三维数组 >>> 一本书（多页纸）

四维数组 >>> 书架（多本书）

五维数组 >>> 图书室 2201（多个书架）

六维数组 >>> 图书馆某一层，2楼/3楼（多个图书室）

七维数组 >>> 整个图书馆

…

…

第 N 维数组 >>> … 宇宙 …

| ================================================== Split Line =============================================== |

👇👇👇 关于 Ndarray 中的一维行向量、列向量的理解 👇👇👇

你可能听过这样的说法：“写数组的时候是横着写的，而其实数组是列向量（更直观）”。

许久以来都有一个疑问 >>> NumPy 中的一维向量究竟是 行向量 还是 列向量 呢？？？

↓↓↓↓↓↓ 测试思路（向量点乘维度要对应的特性） ↓↓↓↓↓↓

1. 构建一个 4*2 的数组 arr 和一个一维的长度为 2 的 Numpy 向量 vec；
2. 使用 arr 点乘 vec >>> 点乘 np.dot(arr, vec) 不报错，说明一维向量为 2*1 的列向量；如果报错，说明向量肯定不是列向量。
3. 如果不报错，先将 vec 转置，然后继续使用点乘 np.dot(arr, vec) >>> 如果还不报错，说明一维向量 vec 既可以当做列向量也可以当做行向量。

先来进行第 1 && 2 步测试：

>>> import numpy as np

>>> arr = np.array([[1, 1, 1, 1], [1, 1, 1, 1]]).T
>>> arr
array([[1, 1],
       [1, 1],
       [1, 1],
       [1, 1]])
>>> arr.shape
(4, 2)

>>> vec = np.array([2, 3])
>>> vec
array([2, 3])
>>> vec.shape
(2,)

>>> np.dot(arr, vec)
array([5, 5, 5, 5])

可见，一维向量 vec 可以作为列向量与矩阵 arr 相乘。

继续进行第 3 步测试：

>>> import numpy as np

>>> arr = np.array([[1, 1, 1, 1], [1, 1, 1, 1]]).T
>>> arr
array([[1, 1],
       [1, 1],
       [1, 1],
       [1, 1]])
>>> arr.shape
(4, 2)
>>> vec = np.array([2, 3]).T
>>> vec
array([2, 3])
>>> vec.shape
(2,)
>>> np.dot(arr, vec)
array([5, 5, 5, 5])

居然也可以进行点乘，Amazing！！！说明 NumPy 中的一维向量既可以作为行向量，也可以作为列向量存在。

总结下来，可以得到如下结论：

[1] >>>> 一维数组的转置仍是自己本身，这点根据上述实验的一维向量 vec 的 shape 就能看出来，vec.T（转置后）维度不变。

[2] >>>> NumPy 中的一维向量，可以认为它既不是行向量也不是列向量，只是一个长度为 2 的一维向量。也可以把理解为它既可以做行向量同时也能做列向量，具体是行向量还是列向量根据与他进行点乘的矩阵而定。

[3] >>>> NumPy 一维向量既可以做行向量也可以做列向量，对于任意一个给定的一维向量，你无法确定它到底是行向量还是列向量。故，习惯上用二维矩阵而不是一维矩阵来表示行向量和列向量，因为二维必定能够确定他是行向量还是列向量。

对于 3，见下例：

# 行向量：
>>> row_vec = np.array([[2, 3]])
>>> row_vec
array([[2, 3]])
>>> row_vec.shape
(1, 2)

# 列向量：
>>> col_vec = np.array([[2], [3]])
>>> col_vec
array([[2],
       [3]])
>>> col_vec.shape
(2, 1)

---

Ndarray 属性详解

这一章节，我们将深入了解 Ndarray 数组中行列优先、维度、轴、形状，以及维间距等…

C/F Order

前面提到过，Ndarray 数组中有一个 order 属性，是指数组的内存布局，常见的有：C-Order(行优先) && Fortran-Order（列优先）。

其中，C-Order 是指类似于 C 语言中数组内存布局，而 Fortran-Order 是指类似于 Fortran 语言数组内存布局。

那么 >>>> Fortran 的列优先是什么含义，与 C 语言行优先有何区别？？？

| ================================================== Split Line =============================================== |

Fortran 也好，C 也好，操作的数组都存在于内存中，而 内存中是没有行列概念的。一维/二维/三维数组，都是 “一条线（序列）” 一样的存储在内存中。在这个层面上，Fortran 与 C 没有区别。

如下范例，内存中存储了 8 个数据：1，2，3，4，5，6，7，8（蓝色框）。

假设（真实地址相似） >>> 由于数组中元素数据类型相同，每个元素所占的字节数固定（int32 && float32），为 4 个字节。它们对应内存中的地址为（连续内存区）：

0x0041F100 , 0x0041F104 , 0x0041F108 ...... 0x0041F11C

不同的是，Fortran 和 C 会以不同的命名习惯来对内存中的数据进行 “命名” 以实现索引，并通过各自的习惯来寻找对应的地址（索引）。

这是由于高级语言通常不会直接访问内存地址，所以 Fortran 和 C 使用数组来 “命名” 这些内存地址，并且通过（数组 + 下标）的索引方式来访问这些内存地址。

1D-Ndarray >>> 如果把这一段内存地址视为 8 元素的一维数组，Fortran 和 C 的规则差别不大，Fortran 默认以 1 开头，而 C 则以 0 开头（索引）<<<< Ndarray 都是从零开始。

2D-Ndarray >>> 如果把这一段内存地址视为 2*4 元素的二维数组，则 Fortran 和 C 还有另一个差异（结合示意图理解）：

• Fortran 会先变化前面的维度，即顺序为 a(1,1) , a(2,1) .... 前面的 1 先变化为 2，后面维度始终保持为 1。直到循环完毕后，再将后面的维度加一，即 a(1,2) , a(2,2).....；
• C 语言则相反，会先变化后面的维度，即顺序为 a[0][0] , a[0][1] .... 后面的 0 先变化为 1，前面维度始终保持为 0。直到循环完毕后，再将前面的维度加一，即 a[1][0] , a[1][1].....。

因此，对于二维数组来说，Fortran 的 a(m, n) 默认情况下，对应于 C 语言的 a[n-1][m-1]。

从 Ndarray 设计哲学来看，C/F Order 是对于 Memory Block 中数据的一种解释方式~~~

---

可见，对于数组中行列的说法很容易混淆。并且，对于高维数组是不存在真正的行和列的，轴（axis）才是始终有意义的表达方式。

维度/轴（Axis）

事实上，对于 Ndarray 轴和维度的概念是通用的。

以三维数组为例，其包含列（Row）、行（Col）、页（Page）三个维度 >>>

再来看其轴（axis），它包括 0、1、2 三个轴（即 axis=0 && axis=1 && axis=2）。其中，axis=0 代表的是页（Page）这一维；axis=1 代表的是列（Row）这一维；axis=2 代表的是行（Col）这一维。

也就是说，axis 越小，其代表的层次（维度）越高。

你应该记得，前面我们说过：对于多维数组（N-Dim）的显示结果和与列表（List）相同，每多嵌套一层，就代表多一个维度（凭借此你可以很轻易的判断出某个 ndarray 数组的维度）。

简单来说，就是 “最外面的括号代表着 axis=0，依次往里的括号对应的 axis 的计数就依次加 1”。

| ================================================== Split Line =============================================== |

↓↓↓↓↓↓ 2D Ndarray ↓↓↓↓↓↓

举个例子，假设二维 ndarray 数组：[[0, 1], [2, 3]]，其 axis 的对应方式就是：

相应轴上的求和（sum）运算推理（确认各轴上元素，求和），先以二维数组为例：

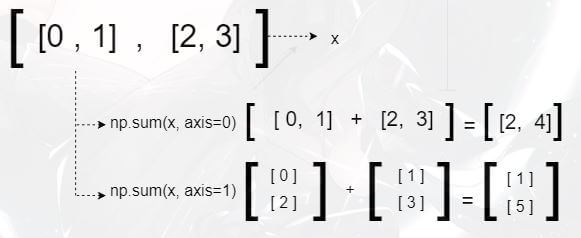
各轴元素对应情况解析 >>>

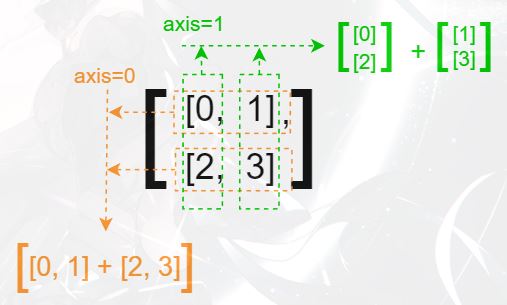
代码验证上述推论过程：

>>> x = np.arange(4).reshape(2, 2)
>>> x
array([[0, 1],
       [2, 3]])

# Axis 0:
>>> np.sum(x, axis=0)
array([2, 4])
# Axis 1:
>>> np.sum(x, axis=1)
array([1, 5])

哎？！！貌似出来的结果比我们推导的结果的括号要少一些。这是因为诸如 np.sum 这种函数中有一个参数叫 keepdims，其默认值是 False，此时它会把多余的括号给删掉。假如我们把它设为 True 的话，就可以得到和推导中一致的结果了：

>>> np.sum(x, axis=0, keepdims=True)
array([[2, 4]])

>>> np.sum(x, axis=1, keepdims=True)
array([[1],
       [5]])

| ================================================== Split Line =============================================== |

↓↓↓↓↓↓ 3D Ndarray ↓↓↓↓↓↓

下面来看一个更 “高维” 一点的样例（三维）：

代码验证上述推论过程：

>>> x = np.arange(8).reshape((2, 2, 2))
>>> x
array([[[0, 1],
        [2, 3]],

       [[4, 5],
        [6, 7]]])

# Axis 0:
>>> np.sum(x, axis=0)
array([[ 4,  6],
       [ 8, 10]])
# Axis 1:
>>> np.sum(x, axis=1)
array([[ 2,  4],
       [10, 12]])
# Axis 2:
>>> np.sum(x, axis=2)
array([[ 1,  5],
       [ 9, 13]])

以及：

# Axis 0:
>>> np.sum(x, axis=0, keepdims=True)
array([[[ 4,  6],
        [ 8, 10]]])
# Axis 1:
>>> np.sum(x, axis=1, keepdims=True)
array([[[ 2,  4]],

       [[10, 12]]])
# Axis 2:
>>> np.sum(x, axis=2, keepdims=True)
array([[[ 1],
        [ 5]],

       [[ 9],
        [13]]])

---

形状（Shape）

通过对 Ndarray 维度/轴的认识，我们已经知道 >>>> 哪个 axis 对应于数组中的哪些元素。

接下来，通过 ndarray.transpose 转置函数来认识一下数组形状（Shape）的本质。

从纸面上来看，如果一个高维数组 arr 的 shape 是 (2, 3, 4)，那么 transpose 的作用就是把这个 shape 中各个数的顺序改一改。如下：

>>> import numpy as np
>>> arr = np.arange(24).reshape((2, 3, 4))
>>> arr
array([[[ 0,  1,  2,  3],
        [ 4,  5,  6,  7],
        [ 8,  9, 10, 11]],

       [[12, 13, 14, 15],
        [16, 17, 18, 19],
        [20, 21, 22, 23]]])
>>> arr.shape
(2, 3, 4)

>>> arr.transpose(1, 0, 2).shape
(3, 2, 4)

可以看到 >>>> 数组 shape 中的各个数就是对应 axis 上的元素个数（层次由高到低）。

如上述实例中数组 arr，其示意图如下：

↓↓↓↓↓↓ 换一种思路理解 ↓↓↓↓↓↓

数组 arr 中共有 24 个元素 >>>>

在 axis=0 轴上，只有两个元素（橙色矩阵）。可以理解为：在 axis=0 这个 axis 上，每隔 24 / 2 = 12 个数就跳一下。

在 axis=1 轴上，由于一个橙色矩阵中只有 24 / 2 = 12 个数。可以理解为：在 axis=1 这个 axis 上，每隔 12 / 3 = 4 个数就跳一下。

在 axis=2 轴上，由于一个蓝色向量中只有 12 / 3 = 4 个数。可以理解为：在 axis=2 这个 axis 上，每隔 4 / 4 = 1 个数就跳一下。

哎，我们得到一个元组 >>> (12, 4, 1) <<< 这就是维间距/步幅（Strides） <<< 记录了每个 axis 上跳过的数。

| ================================================== Split Line =============================================== |

激动人心的时刻到了：

transpose 的本质，其实就是对 axis/shape/strides 中各个数的顺序进行调换（换轴）。如上实例：

>>> x.transpose(1, 0, 2)
array([[[ 0,  1,  2,  3],
        [12, 13, 14, 15]],

       [[ 4,  5,  6,  7],
        [16, 17, 18, 19]],

       [[ 8,  9, 10, 11],
        [20, 21, 22, 23]]])

在 transpose(1, 0, 2) 后，相应的 strides 会变成 (4, 12, 1)。而从上图可以看出，transpose 的结果确实满足：

• axis=0 的 axis 上，每隔 4 个数跳一下；
• axis=1 的 axis 上，每隔 12 个数跳一下；
• axis=2 的 axis 上，每隔 1 个数跳一下。

👇👇👇 需要注意 👇👇👇

有没有同学计算之后，认为换轴后 strides 会变成 (8, 4, 1)？？？

你需要注意的是，数组中数据元素是在一个连续的 Memory Block（[0, 1, 2, 3, 4, ..., 23]）存储的，而 transpose 仅是数据的一种解释行为，数据元素序列是不会变化的！！！

以 axis=0 轴为例，每隔 4 个数跳一下，指的是 >>> 元素序列上元素每隔 4 个数跳一下，即跳到 axis=0 轴下一个元素 >>> [0, 1, 2, 3] --> [4, 5, 6, 7] -->[8, 9, 10, 11]。

---

维间距/步幅（Strides）

我们知道的是，执行换轴操作（transpose）后，会同时引发数组形状（Shape）和步幅（Strides）的变化，这是必然的！！！

代码验证上述推论过程：

>>> import numpy as np
>>> x = np.arange(24).reshape([2, 3, 4])
>>> x
array([[[ 0,  1,  2,  3],
        [ 4,  5,  6,  7],
        [ 8,  9, 10, 11]],

       [[12, 13, 14, 15],
        [16, 17, 18, 19],
        [20, 21, 22, 23]]])

>>> x.shape
(2, 3, 4)
>>> x.transpose(1, 0, 2).shape
(3, 2, 4)

>>> x.strides
(48, 16, 4)
>>> x.transpose(1, 0, 2).strides
(16, 48, 4)

哎，怎么和上面实例提到的 Strides 不一样啊？！！

事实上，维间距/步幅（Strides）记录的是 >>>> 每个 axis 轴上跳过的字节数（Bytes）。

所以，你需要在上面的基础上乘以每个元素的字节大小，验证一下：

>>> x.itemsize
4

>>> before_strides = [int(item / x.itemsize) for item in (x.strides)]
>>> before_strides
[12, 4, 1]
>>> before_strides = [int(item / x.itemsize) for item in (x.transpose(1, 0, 2).strides)]
>>> before_strides
[4, 12, 1]

👇👇👇 总结一下 👇👇👇

数组 x 以 96(24 个值 * 4 = 96) 个字节的形式存储在内存中，一个接一个(连续内存块)。数组的维间距/步幅告诉我们 >>> 要沿着某个轴移到下一个位置，需要在内存中跳过多少个字节。

---

偏移量（Offset）

有时候，你会见到元素偏移量的说法，这里也来简单认识一下。

对于数组元素偏移量 >>>> 当前数组元素的地址 与 数组首地址 的差值。 <<<< 相对于首元素的偏移

↓↓↓↓↓↓ 一维数组：A[N] ↓↓↓↓↓↓

对于一维数组，索引即偏移。

↓↓↓↓↓↓ 二维数组：A[M][N] ↓↓↓↓↓↓

对于任一元素 A[i][j] 的偏移量的计算方法就是：i*N+j。

↓↓↓↓↓↓ 三维数组：A[O][M][N] ↓↓↓↓↓↓

对于任一元素 A[i][j][k] 的偏移量的计算方法就是：i*M*N + j*N + k。

很好理解，不多解释~~~

---

参考链接：

https://blog.csdn.net/zengmingen/article/details/106894280
https://www.cnblogs.com/shine-lee/p/12293097.html
https://zhuanlan.zhihu.com/p/199615109
https://blog.csdn.net/doubleguy/article/details/121566140
https://blog.csdn.net/qq_34035425/article/details/123251659
https://blog.csdn.net/pql925/article/details/84583236
https://blog.csdn.net/qq_43320208/article/details/121509309