The Pixel Matrix Representation Of Image

在计算机视觉中，图像是以像素矩阵（Image Pixel Matrix）的形式进行表示和处理的。

计算机视觉

我们知道，图像（图片）是 三维现实场景的二维表示。

一切看似复杂的计算机视觉项目，其基础都会回归到单张（灰度/彩色/黑白）图像上。

那么，计算机是如何认识以及处理图像数据的？！！

---

像素网格

如果你在某个观景处拍张照片，就可以得到它的二维图像，这是计算机 “看” 图的第一步。

这张图像包含的信息有：景物的颜色、形状、表观大小（随摄影距离的远近，物体表现得更大还是更小），以及随照明条件的不同而产生的不同阴影等。（为了避免彩色带来的复杂性，这里将通过其灰度图像进行说明）

此时，如果你一直放大图片中的某一小部分，最终会发现 >>>> 原来，计算机中图像是由一个个小块（这就是像素）组成的二维网格（像素网格）：

事实上，像素网格中的每个像素都有一个对应的数值（像素值），取值范围是 0~255（其中，0 表示最暗黑色；255 表示最亮白色）。

这样，就可以通过定位像素网格的横纵坐标来获取某一特定位置的像素值：

哎~~~~ 像素网格这不就和矩阵（Matrix）高度吻合了么？，像素网格中的每一个像素对应矩阵的元素！！！

---

从像素网格到像素矩阵（Pixel Matrix）：

像素矩阵

可以很容易想到 >>>> 图像中的尺寸，有着宽度（width）和高度（height），而矩阵有着对应的行（row）和列（column）定义。矩阵中的每一个元素对应图像中的像素。

这样，我们就完成了：图像 >>>> 像素网格 >>>> 像素矩阵 的 “映射” 分析。

实际上，图像在计算机中的处理，就是 将对图像的操作转换成对图像像素矩阵的操作（计算机中矩阵的操作是非常常见且成熟的）。事实上所有的图像处理工具都是这么做的。

这里，将使用 Python 图像处理库 OpenCV 提供的方法来进行简单的图像读取和处理演示。

[1] >>> 图像读取和查看

import cv2

# 读取图像，并设置为灰度图（0）
mountain = cv2.imread('mountain.png', 0)

# 查看图像读取后像素矩阵的数据类型：
print ("type:", type(mountain))
# type: <class 'numpy.ndarray'>

# 查看图像的尺寸（像素矩阵的形状）：
print ("shape:", mountain.shape)
# shape: (480, 640)

可以看到，图像读取后，被存储到 NumPy 中的 ndarray 数组中。其中，图像的像素矩阵行（row）为 480 px，列（column）为 640 px；分别对应原始图像中的高度（width）和宽度（height）。

[2] >>> 获取特定位置的像素值

print(mountain[100, 100])
# 236

可在，在像素矩阵中（100, 100）位置处的像素值为：236。

[3] >>> 图像裁剪操作

对图像像素矩阵的操作就是对原始图像的操作。例如选取像素矩阵中某个区域的值，也就是所谓的 Crop（图像裁剪）操作：

print (mountain[9:12, 9:12])

输出以下子矩阵：

[[244 244 244]
 [244 236 244]
 [244 244 236]]

我们来重新截取，并且显示一下截取到的图像：

# 取大一些的区域，并显示出来。
crop_image = mountain[200:400, 200:600]
cv2.imshow("crop", crop_image)

# 存储裁剪后的图像，并查看其像素矩阵：
cv2.imwrite("crop_image.png", crop_image)
print(crop_image.shape)
print(crop_image)
cv2.waitKey()

裁剪区域的像素矩阵如下：

[[132 236 228 ... 116  84  28]
 [228 204 220 ... 116  92  76]
 [172 132 116 ...  92 116  76]
 ...
 [172 140  92 ...   4  28  28]
 [180 228 180 ...   4   4   4]
 [132 148  84 ...  28   4  28]]

裁剪到的子图像如下：

最后再重新读取进来查看一下裁剪到的子图像所对应的矩阵：

mountain_crop = cv2.imread('crop_image.png', 0)
print ('Shape:', mountain_crop.shape)
print ('Image Pix Matrix:','\n', mountain_crop)

输出如下（结果和上述操作完全一致）：

Shape: (200, 400)
Pix Matrix: 
 [[132 236 228 ... 116  84  28]
 [228 204 220 ... 116  92  76]
 [172 132 116 ...  92 116  76]
 ...
 [172 140  92 ...   4  28  28]
 [180 228 180 ...   4   4   4]
 [132 148  84 ...  28   4  28]]

---

RGB 色彩通道

上面为了避免图像彩色带来的复杂性，仅通过灰度图像引出像素矩阵（Pixel Matrix）的概念，这里我们重新来看彩色图像的像素矩阵。

毋庸置疑，彩色图像比灰度图像拥有更多的信息，如图：

通过 Python 图像处理库 OpenCV 查看其像素矩阵信息：

import cv2
drawing = cv2.imread('color_image.png')

print ("type:", type(drawing))
# type: <class 'numpy.ndarray'>
print ("shape:", drawing.shape)
# shape: (309, 600, 3)

print ("Pixel Value: ", drawing[100, 100])
# Pixel Value:  [58 19 55]

可以看出，彩色图像读取后仍然是 Ndarray 数组（但变为了 3 维）。不同的是，彩色图像像素矩阵中某个像素点的值成为一个包含 3 个数值的数组，如何理解？！！

---

三维堆叠像素矩阵

从上可以看出，计算机中，灰度图像是只有长和宽的二维像素矩阵，而彩色图像是三维堆叠像素矩阵。

事实上，彩色图像会被解析为具有宽（width）、高（height）和色彩通道（channel）的三维堆叠像素矩阵。从数组角度理解，axis=0 轴对应图像的色彩通道，axis=1 轴对应图像的高，axis=2 轴对应图像的宽。0 轴上的每一个元素都表征一个特定色彩通道（R/G/B）的像素矩阵。

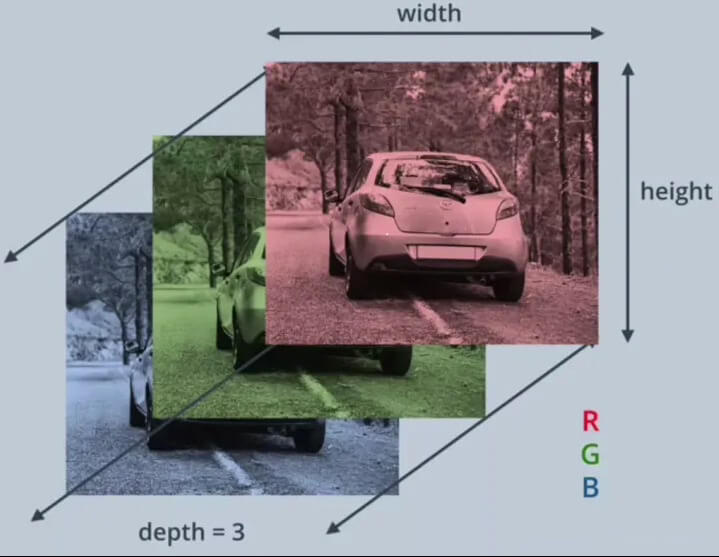
引入色彩通道，是由于大多数彩色图像可以仅通过三种颜色（三原色 >>>> 红：Red，绿：Green，蓝：Blue）组合来表示，就是我们常说的 RGB。

故，彩色图像的像素矩阵，可以看作 >>>> 三个表征不同色彩（R/G/B）的二维色彩图层堆叠而成！！！因此，获取图像中某像素位置处的像素值取到是包含 3 个值的数组，分别代表该像素点处的 R、G、B 值。

或者，你可以还可以理解为 >>>> 彩色图像的像素矩阵中的，任一像素点都可以分解为 R、G、B 三个基色分量！！！

---

二维 RGB 色彩图层

深入来看一下 RGB 各个色彩图层究竟是什么样子的？！！

需要注意的是，Python OpenCV 读取彩色图像对应的像素矩阵中顺序是 BGR。下面我们抽离出各通道矩阵来查看其图像：

import matplotlib.pyplot as plt
%matplotlib inline
import cv2

original = cv2.imread('color_image.png') # BGR
original = cv2.cvtColor(original, cv2.COLOR_BGR2RGB) # BGR To RGB

# 抽离各色彩通道（R/G/B）的像素矩阵：
pixMatrix_all = [original, original[:, :, 0], original[:, :, 1], original[:, :, 2]]
channels = ["RGB", "red", "green", "blue"]

for i in range(4):
    plt.subplot(2, 2, i + 1)
    plt.imshow(pixMatrix_all[i], cmap=plt.cm.gray)
    plt.title(channels[i])
plt.show()

# for item in pixMatrix_all:
#     print(item.shape)

可视化输出如下：

可以看出，抽离出的各色彩通道像素矩阵的灰度图，均为原始图像的完整图像，但细节处存在一定的差异。

为了更贴近彩色图像的像素矩阵表示，你可以将抽离出的各色彩通道像素矩阵转化为三通道彩色图：

import matplotlib.pyplot as plt
%matplotlib inline
import numpy as np
import cv2

original = cv2.imread('color_image.png')  # BGR
original = cv2.cvtColor(original, cv2.COLOR_BGR2RGB)  # BGR To RGB

# 各通道的图像是一张灰度图，这里我们将其转化为三通道彩色图:
red = np.zeros_like(original)
red[..., 0] = original[..., 0]
green = np.zeros_like(original)
green[..., 1] = original[..., 1]
blue = np.zeros_like(original)
blue[..., 2] = original[..., 2]

pixMatrix_all = [original, red, green, blue]

channels = ["RGB", "red", "green", "blue"]
for i in range(4):
    plt.subplot(2, 2, i + 1)
    plt.imshow(pixMatrix_all[i])
    plt.title(channels[i])
plt.show()
#for index in pixMatrix_all:
#    print(index.shape)

可视化输出如下：

可以看出，每一个 RGB 通道都是一个像素矩阵。这 3 个 RGB 通道堆叠在一起形成了彩色图像~~~

---

灰度、灰度级与位深度

最近刚开始学数字图像处理，以为灰度只是表示黑白/深浅色图像。事实上，灰度（灰度值）只是表征单色的亮暗程度！！！灰度（灰度值）越大表示当前单色越亮。

例如，在黑白显示器中单指像素点显示的亮暗差别；而在彩色显示器中也表征像素点在不同色彩通道的亮暗程度，但不同亮暗程度 R/G/B 色彩分量的组合又表现为颜色的不同。灰度值越多，表现颜色越多，图像层次越清楚逼真。

而，灰度级 >>>> 取决于图像中每个像素点对应的存储单元位数（bit），限制了灰度（灰度值）的取值范围。

例如，某灰度图像中每个像素使用 8 位二进制存储（8 bit），其灰度级为 2^8 = 256，灰度值范围（亮暗范围）为 (0~255)，也对应当前单色的 256 种亮暗变化色。

位深度 >>>> 即像素点存储单元位数（bit）。这就是我们常说的 8 位图、16 位图以及 32 位图等。

位深度和灰度级满足如下关系（其中，K 为位深度，L 为灰度级）：

$$ L = 2^{k} $$

通常，图像像素矩阵中的灰度值位于图像可正常显示的整数范围 [0, L-1]。有时，出于算法开发以及计算的目的，你还会遇到对图像进行归一化的操作，它是将图像像素矩阵中的灰度值压缩到 [0, 1]。

| ================================================== Split Line =============================================== |

👇👇👇 常见位深度彩色图像 👇👇👇

各个色彩通道（R/G/B）上的灰度值范围由其所占用位数决定，对应各单色的亮暗变化色数量：

[1] >>> 8 位图像

存储一个像素需要内存：1 Byte

R:G:B = 2:3:3

可显示颜色：$$ 2^{8} = 2^{2}(B) * 2^{3}(G) * 2^{3}(R) $$

灰度级：255(2^8)

[2] >>> 16 位图像

存储一个像素需要内存：2 Byte

R:G:B = 5:6:5

可显示颜色：$$ 2^{16} = 2^{5}(B) * 2^{6}(G) * 2^{5}(R) $$

灰度级：65533(2^16)

[3] >>> 24 位图像

存储一个像素需要内存：3 Byte

R:G:B = 8:8:8

可显示颜色：$$ 2^{24} = 2^{8}(B) * 2^{8}(G) * 2^{8}(R) $$

灰度级：2^24

[4] >>> 32 位图像

存储一个像素需要内存：4 Byte

32 位图像：Alpha 透明度通道 + 24 位

| ================================================== Split Line =============================================== |

由上就可以计算，图像文件未经压缩的字节数 = 图像分辨率 * (位深度/8)。

例如，一幅分辨率为（640*480），位深度为 24 bit 的图像，其图像未经压缩的数据容量为：640 * 480 * (24 /8) = 900KB。

为什么要强调图像未经压缩？！！

这是由于，一张图片可以被保存为很多种不同的格式，例如：bmp/png/jpeg/gif，不同格式文件的压缩品质不同，还有的文件要记录操作信息（图层、通道等），所以上述只是基本的原理算法。

---

灰度/彩色/黑白图像

通过上面的说明，相信你对灰度图像、彩色图像的差异有了一定的认知。这里重新阐述一下：

彩色图像

彩色图像不同多说，其像素矩阵是由三个表征不同色彩（R/G/B）的二维色彩图层堆叠而成（三通道），也就说任一像素点都可以分解为 R、G、B 三个基色分量。

每个基色分量上的灰度值，直接决定了其基色的明暗强度！！！

| ================================================== Split Line =============================================== |

灰度图像

灰度图像，通常显示为从最暗黑色（0）到最亮的白色（255）的灰度（如下图）。

其像素矩阵就是一个单色的灰度值矩阵（单通道），灰度值表征单个像素点的亮度。

| ================================================== Split Line =============================================== |

黑白图像

黑白图像，也叫二值图像，是一种特殊的灰度图像。

与灰度图像不同的是，黑白图像中每个像素的灰度值仅能取 0 或者 255，分别代表纯黑和纯白。

需要注意的是，单通道图像一定没有彩色；没有彩色的图像不一定是单通道的灰度/黑白图像，比如所有像素分量均为 0 的纯黑彩色图像。

---

图像灰度化/二值化处理

大多数的计算机视觉场景下，灰度/黑白图像已经够用了。

故，一般会对原始图像进行灰度化/二值化处理，生成其灰度/黑白图片，减小了参与运算的图像像素矩阵的规模，可以提高算法的计算性能。

[1] >>> 灰度化处理

常用灰度化处理的方法：

1. 浮点算法：Gray = R*0.3 + G*0.59 + B*0.11；

2. 整数方法：Gray = (R*30 + G*59 + B*11) / 100；

3. 移位方法：Gray = (R*28 + G*151 + B*77) >> 8；

4. 平均值法：Gray =（R + G + B）/ 3；

5. 仅取绿色：Gray = G，图像中绿色通道的信息最全面。

| ================================================== Split Line =============================================== |

[2] >>> 二值化处理

二值化就是让图像的像素点矩阵中的每个像素点的灰度值为 0（黑色）或者 255（白色），也就是让整个图像呈现只有黑和白的效果。

那么一个像素点在灰度化之后的灰度值怎么转化为 0 或者 255 呢？？？比如灰度值为 100，那么在二值化后到底是 0 还是 255 ？！！

↓↓↓↓↓↓ 需要借助阀值来实现 ↓↓↓↓↓↓

1、取阀值为 127（相当于 0~255 的中数，（0+255）/2=127），让灰度值小于等于 127 的变为 0，灰度值大于 127 的变为 255。好处 >>>> 计算量小速度快；缺点 >>>> 因为这个阀值在不同的图片中均为 127，但不同图片的颜色分布差别很大，白菜萝卜一刀切的效果肯定是不好的。

2、像素矩阵中像素点的灰度值的平均值 avg 作为阈值，让灰度值小于等于 avg 的像素点就为 0，灰度值大于 avg 的变为 255。效果要由于方法一。

3、直方图方法（双峰法）来寻找二值化阀值。直方图方法认为图像由前景和背景组成，在灰度直方图上，前景和背景都形成高峰，在双峰之间的最低谷处就是阀值所在。取到阀值之后再一一比较就可以了。

---

彩色 Or 灰度/黑白？？？

上一小节说到，大多数的计算机视觉场景下，灰度/黑白图像已经够用了。为什么还需要彩色图像？！！

尽管彩色图像带来了不必要的复杂性且占用了更多的内存空间，但在某些任务中，图像色彩信息会非常有用！！！例如，识别交通道路线中的黄白线时，色彩就显得尤为重要了。

那么，到底什么时候需要保留色彩信息呢？？？

原则 >>>> 在计算机视觉应用中，如果对人眼来说，彩色图像识别起来更轻松，那么彩色图像对算法来说也更轻松些。

一言以蔽之，如果色彩的存在对最终的结果非常有帮助，那就用吧！！！

---

深入解析 RGB 图像灰度与通道

彩色图像/RGB 图像中，图像是一个三维矩阵，如：(244, 780, 3)，其中 244 表示行数（高），780 表示列数（宽），3 代表三个基色分量（R/G/B）。如下：

每一层矩阵（244, 780, 0/1/2），分别对应 R/G/B 的灰度值像素矩阵。仅仅表示对应单色光灰度值，不是彩色的图像。如下：

import matplotlib.pyplot as plt
%matplotlib inline
import numpy as np
import cv2

original = cv2.imread('red_vs_white.jpg') # BGR
original = cv2.cvtColor(original, cv2.COLOR_BGR2RGB) # BGR To RGB

# 抽离各色彩通道（R/G/B）的像素矩阵：
original_all = [original, original[:, :, 0], original[:, :, 1], original[:, :, 2]]
channels = ["RGB", "red", "green", "blue"]

for i in range(4):
    plt.subplot(2, 2, i + 1)
    plt.imshow(original_all[i], cmap=plt.cm.gray)
    plt.title(channels[i])
plt.show()

# for item in original_all:
    # print(item.shape)

可视化结果如下：

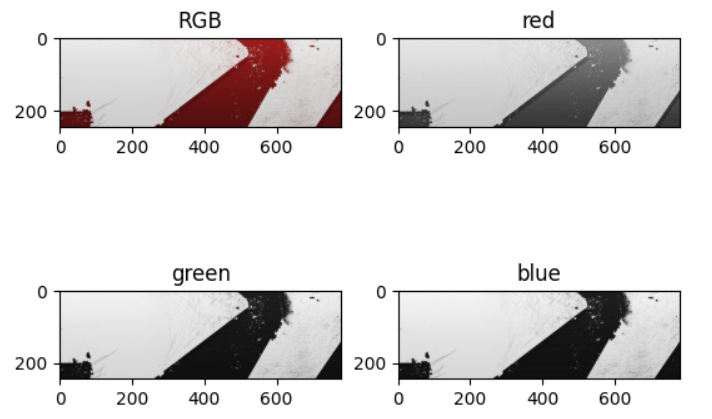
色彩通道类似颜料（基色），想要什么颜色，对应的通道里的灰度值就大一点就行了。如上图，随便在红色区域上取一个样点 (200, 400)，其灰度值分别是（R:94, G:18,B:18）。

print(original[200, 400])
# [94 18 18]

所以在显示的时候，红色通道里灰度值大，绿色通道和蓝色通道里的灰度值小，显示出来的就是红色。

如果我们交换一下分量放置的顺序，把 G 分量放进红色通道里，把 R 分量放进绿色通道里，B 分量放进蓝色通道里，会怎么样呢？？？

new_img = np.zeros_like(original)
new_img[..., 0] = original[..., 1]
new_img[..., 1] = original[..., 0]
new_img[..., 2] = original[..., 2]
plt.imshow(new_img)
plt.show()

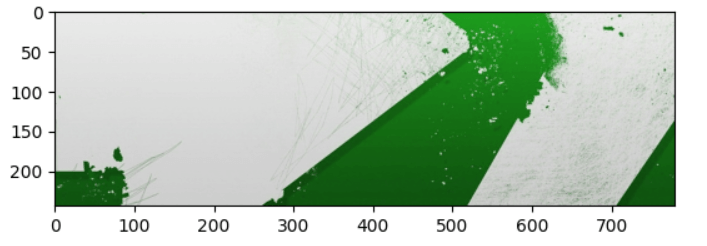
此时绿通道中的灰度值最大，红色通道和蓝色通道中的灰度值都较低，显示为绿色。

同理，如果把 B 分量放进红色通道里，把 R 分量放进蓝色通道里，G 分量放进绿色通道里，会怎么样呢？？？

new_img = np.zeros_like(original)
new_img[..., 0] = original[..., 2]
new_img[..., 1] = original[..., 1]
new_img[..., 2] = original[..., 0]
plt.imshow(new_img)
plt.show()

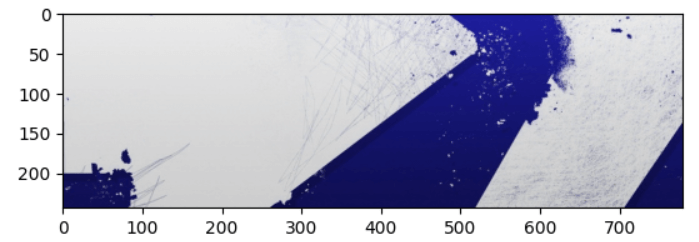
事实上，我们熟知的 RGB 色彩空间，就是把一种颜色，用 RGB 三个分量表达出来。此外还有 CMYK（四个分量）、Lab（三个）、HSV（三个）等等。不同色彩空间之间的关系，类似于空间直角坐标系（x, y, z），球坐标系（r, φ, θ）或柱坐标（r, φ, z）之间的关系。

---

https://blog.csdn.net/Dontla/article/details/106897794
https://blog.csdn.net/qq_41498261/article/details/104898045
https://blog.csdn.net/gaoxueyi551/article/details/112684581
https://blog.csdn.net/Strive_0902/article/details/78023080
https://zhuanlan.zhihu.com/p/427723550
https://blog.csdn.net/weixin_44489823/article/details/105996194