TensorFlow 入门之 TF 基本工作原理

前面，我们已经成功搭建了基于 TensorFlow 的深度学习框架环境，并完成一个简单的向量加法实例。本篇我们将正式开始 TenosorFLow 相关概念的学习。

配置过程中参考了网络上很多的相关博文，也遇到过很多坑，为了感谢配置过程中各位大佬的帮助以及方便本人下次配置或者升级，整理以作此文。

更多 TensorFlow 框架学习相关内容，请关注博主相关博文系列 ↓↓↓↓↓

之一 >>>> 一文详解全平台 TensorFlow 深度学习框架在线搭建 (CPU&GPU 支持)

之二 >>>> TensorFlow GPU 支持: Ubuntu16.04 + Nvidia GTX + CUDA + CUDNN

之三 >>>> TensorFlow 入门之 TF 基本工作原理

之四 >>>> TensorFlow 入门之深度学习和深层神经网络

之五 >>>> TensorFlow 入门之 MNIST 手写体数字识别问题

之六 >>>> TensorFlow 入门之图像识别和卷积神经网络（CNN）

| ================================================== Split Line =============================================== |

本篇，我们将通过两部分内容详细介绍 TensorFlow 的基本工作原理：

• 第一部分 >>> 分别通过 TensorFlow 的 计算模型（Graph：计算图）、数据模型（Tensor：张量）以及运行模型（Session：会话），帮助我们对 TensorFlow 的工作原理有一个基本的了解；
• 第二部分 >>> 我们将简单介绍神经网络的基本概念，主要计算流程，以及如何通过 TensorFlow 来实现神经网络计算过程。

---

TF 基本工作原理

TensorFlow 见名知义：Tensor（张量） 和 Flow（流），表达了它最重要的两个概念：

第一个词 Tensor，就是张量（属于数学或物理中的概念，这里不强调其本身的含义），可以被简单理解为多维数组，表达了 TensorFlow 的数据模型；第二个词 Flow，就是流（数据的流动或转化）它直观的表达了数据（张量）之间通过计算相互转换的过程。

TF 计算模型（Graph：计算图）

计算图（Graph）是 TensorFlow 中最基本的一个概念。

Tensorflow 是一个通过计算图的形式表述计算的编程系统，也就是说，所有的 TensorFlow 程序都可以通过计算图的形式来表示。

更深入的理解是 >>> TensorFlow 程序中的所有计算都会被转化为计算图上的节点，计算图中的每一个节点就表示一个计算。计算图中节点之间的边描述了计算之间的依赖关系。

基于上述，下图展示了通过 TensorFlow 可视化工具 TensorBoard 画出的两个向量相加程序样例的计算图：

图中的每一个节点都代表了一个计算 >>> 如 a 节点、b 节点 (TensorFlow 会将常量转化成一种永远输出固定值的运算)以及 add 节点（加法运算）；节点之间的边表示了计算之间的依赖关系，如 add 运算的输入依赖于 a 和 b 运算的输出，而 a 和 b 两个常量不依赖于任何计算。

---

计算图的使用

TensorFlow 程序一般分为两个阶段：

• 第一阶段 >>>> 需要定义计算图中的所有需要执行的运算；
• 第二阶段 >>>> 执行定义好的运算（Session）。

首先来看如何定义 TensorFlow 程序（计算图上）中的所有计算：

这里，首先给出 TensorFlow 向量加法程序样例中，定义计算图中计算节点（a，b，result）的方法：

# 导入 TensorFlow 模块：
import tensorflow as tf

# 定义 TF 常量节点 a && b
a = tf.constant([1.0, 2.00], name="a")
b = tf.constant([3.0, 4.00], name="b")
# 定义加法运算节点：
result = a + b

注意，这里仅仅是定义了相关的运算节点，但程序并未进行计算，需要通过后面章节的 Session 会话进行运行。

| ================================================== Split Line =============================================== |

[1] >>> 默认计算图机制

你可能比较疑惑：上面的样例中，并没有看到任何和计算图定义有关的语句，怎么就使用到计算图（Graph）了？！！

事实上，TensorFlow 程序中，系统会自动为其维护一个默认的计算图（Default Graph），TensorFlow 会自动将定义好的计算转化为 Default 计算图上的节点。如上述向量加法样例中 a、b、以及 result 节点所属计算图即为默认计算图。

↓↓↓↓↓↓ 如何查看 TF 默认、以及某运算节点所属的计算图信息？？？ ↓↓↓↓↓↓

• Tensor.graph：通过张量（Tensor）的 graph 属性可查看其所属的计算图；
• tensorflow.get_default_graph：通过（获取默认计算图方法）可获取到程序当前默认的计算图信息；

样例如下：

# 查看节点 a 所属的计算图：
print (a.graph)
# 查看程序默认的计算图：
print (tf.get_default_graph())
# 判断节点 a 是否属于默认计算图中定义节点：
print (a.graph is tf.get_default_graph())

样例语句输出:

<tensorflow.python.framework.ops.Graph object at 0x00000204B01969E8>
<tensorflow.python.framework.ops.Graph object at 0x00000204B01969E8>
True

[2] >>> 如何自定义计算图

TensorFlow 中支持通过 tf.Graph() 函数来自定义一个新的计算图。实例代码如下：

import tensorflow as tf

g = tf.Graph()

print(g)
# <tensorflow.python.framework.ops.Graph object at 0x0000020206621F48>
print(tf.get_default_graph())
# <tensorflow.python.framework.ops.Graph object at 0x000002020662D308>
print(g is tf.get_default_graph())
# False

可见，我们已经定义了一个新的，区别于默认计算图的 Graph：g。

---

计算图的意义

TensorFlow 中计算图的引用是具有非常重要的意义的：

[1] >>> Graph 隔离张量和计算

在不同的计算图上的张量和运算不会共享，故 Graph 可以用来隔离张量和计算。

样例程序如下所示：

import tensorflow as tf


### 1. 定义计算图中的所有需要执行的运算 ###

g1 = tf.Graph()
# 在计算图 g1 中定义变量 'v'，并初始化为 0 ：
with g1.as_default():
    #  Old Version Error:
    #     v = tf.get_variable(
    #                        "v", initializer=tf.zeros_initializer(shape=[1]))
    #  New Version:
    v = tf.get_variable("v", initializer=tf.zeros_initializer()(shape=[1]))

g2 = tf.Graph()
# 在计算图 g2 中定义变量 'v'，并初始化为 1 ：
with g2.as_default():
    v = tf.get_variable("v", initializer=tf.ones_initializer()(shape=[1]))
    
### 2. 执行定义好的运算 ###

# 在计算图 g1 中读取变量 ‘v’的取值：
with tf.Session(graph=g1) as sess:

    #     Old Version Error:
    #     tf.initializer_all_variables().run()
    #     AttributeError: module 'tensorflow' has no attribute 'initializer_all_variables'
    #     New Version:
    tf.global_variables_initializer().run()
    with tf.variable_scope("", reuse=True):
        # 在计算图 g1 中，变量 'v' 的取值应该为 0，所以这里输出: [0.]
        print (sess.run(tf.get_variable('v')))

# 在计算图 g2 中读取变量 ‘v’的取值：
with tf.Session(graph=g2) as sess:
    tf.global_variables_initializer().run()
    with tf.variable_scope("", reuse=True):
        # 在计算图 g2 中，变量 'v' 的取值应该为 1，所以这里输出: [1.]
        print (sess.run(tf.get_variable('v')))

样例执行结果如下：

[0.]
[1.]

这里，你需要注意 g = tf.Graph() && g.as_default() 和 tf.Session(graph=g) 的用法。

| ================================================== Split Line =============================================== |

[2] >>> Graph 管理运算以及资源

TensorFlow 中的 Graph 不仅仅可以用来隔离张量和计算，还提供了管理张量和计算的机制。

↓↓↓↓↓↓ 管理张量和计算 ↓↓↓↓↓↓

例如，计算图可以通过 tf.Graph.device() 函数来指定执行运算的设备：

# TensorFlow 还提供了对 GPU 的支持，来加速计算。
# 具体使用 GPU 的办法随后章节会介绍，这里我们知道 TensorFlow 支持 GPU 加速的机制即可。
g = tf.Graph()

with g.as_default():
    a = tf.constant([1.0, 2.0], name='a')
    b = tf.constant([2.0, 3.0], name='b')

with g.device('/gpu:0'):
    result = a + b

with tf.Session(graph=g) as sess:
    print (sess.run(result))

注意，tf.Graph().device() 就是 图.device()，可以为某个计算图指定运算的设备。

↓↓↓↓↓↓ 管理程序资源 ↓↓↓↓↓↓

除了管理计算之外，Graph 还能有效管理 TensorFlow 程序中的资源（资源可以是张量、变量或者程序运行时的队列资源等）。

例如：在一个计算图中，可以通过集合（collection）来管理不同类别的资源。比如：通过 tf.add_to_collection(coll_name, var_value) 函数将资源加入到一个或多个集合中； 通过 tf.get_collection(key) 函数来获取一个集合中的所有资源。

为了使用方便，TensorFlow 自动管理了一些常用的集合，如下图所示的几个 TensorFlow 自动维护的集合：

集合名称	集合内容	使用场景
tf.GraphKeys.VARIABLES	所有变量	持久化 TensorFlow 模型
tf.GraphKeys.TRAINABLE_VARIABLES	可学习的变量(一般指神经网络中的参数)	模型训练、生成模型可视化内容
tf.GraphKeys.SUMMARIES	日志生成相关的张量	TensorFlow 计算可视化
tf.GraphKeys.QUEUE_RUNNERS	处理输入的 QueueRunner	输入处理
tf.GraphKeys.MOVING_AVERAGE_VARIABLES	所有计算了滑动平均值的变量	计算变量的滑动平均值

关于上述集合的具体使用不需要深究，在后续相关内容部分会进行说明。

---

这一小节，我们来介绍 TensorFlow 中另一个重要的基本概念：Tensor。

TF 数据模型（Tensor：张量）

张量（Tensor）是 TensorFlow 管理数据的形式，在 TensorFlow 程序中，所有的数据都通过张量的形式表示。

从功能角度来看，张量可以被简单理解为多维数组：零阶张量表示标量（scalar），也就是一个数；第一阶张量表示向量（vector），也就是一个一维数组；第 n 阶张量可以理解为一个 n 维数组。

但是我们要明白，“可以被理解为” 并不是 “实际上就是”！实际上，张量在 TensorFlow 中的实现并不是直接采用数组的形式，它只是一个对 TensorFlow 运算结果的引用，张量中并没有存储真正的数值，它保存的一个运算的过程。

如何理解？？？来看下面的代码，运行后并不会得到加法的结果，而是对结果的一个引用：

import tensorflow as tf

a = tf.constant([1.0, 2.0], name="a")
b = tf.constant([3.0, 4.0], name="b")
result = a + b

print(a)
# Tensor("a:0", shape=(2,), dtype=float32)
print(b)
# Tensor("b:0", shape=(2,), dtype=float32)
print(result)
# Tensor("add:0", shape=(2,), dtype=float32)

可以看出：TensorFlow 中的张量和 Numpy 中的数组是不同的，不是一个数组，不存储数值，而是一个张量结构。

---

根据上面样例输出的张量，接下来我们来看张量结构：

张量结构

从上述结果中可以看出，一个张量结构主要保存了三个属性：名字（name）、维度（shape）以及 类型（dtype）。

[1] >>> 名字（name）

名字，不仅是张量的唯一标识，也给出了张量是如何计算出来的。

我们知道：TensorFlow 程序都可以通过计算图模型来建立，而计算图中的每一个节点都代表的是一个个的计算，计算结果的引用就存储在张量中，所有张量和计算图中的节点是对应的。

这样张量的命名就可以通过 node_name:src_output 的形式给出。 <<< node_name: 表示当前张量对应节点的名称；src_output: 表示当前张量来至对应节点的第几个输出。

例如上面示例中：add:0 表示 result 这个张量是加法节点 add 输出的第一个结果（编号从 0 开始）。

| ================================================== Split Line =============================================== |

[2] >>> 维度（shape）

维度，描述了一个张量的维度信息。维度是张量的一个重要属性，围绕维度 TensorFlow 给出了很多有用的运算，后面我们会涉及到部分相关运算。

例如：shape=(2,) 表示 result 这个张量是一个一维数组，数组的长度为 2。

| ================================================== Split Line =============================================== |

[3] >>> 类型（dtype）

类型，每个张量会有一个 唯一 的类型，TenosorFlow 会对所有参与运算的张量进行类型检查。一旦发现类型不匹配时会报错，如下代码：

import tensorflow as tf

a = tf.constant([1.0, 2.0], name="a")
b = tf.constant([3, 4], name="b")  # 去掉数值后的小数点，会使 b 的类型变为整型
result = a + b

执行上述代码报错：TypeError: Input 'y' of 'Add' Op has type int32 that does not match type float32 of argument 'x'。

Why？！！这是由于 >>>>

TensorFlow 中，如果不指定类型，TensorFlow 会给出默认的类型： 不带小数点的数会被默认为 int32； 带小数点的数会被默认为 float32。

由于使用默认类型可能导致潜在的类型不匹配问题，所以 一般建议通过 dtype 属性来明确指出变量或常量类型。如下：

import tensorflow as tf

a = tf.constant([1.0, 2.0], dtype=tf.float32, name="a")
b = tf.constant([3.0, 4.0], dtype=tf.float32, name="b")
result = a + b

👇👇👇 TensorFlow 中支持的数据类型 👇👇👇

实数型：tf.float32、tf.float64 ；整数型：tf.int8、tf.int16、tf.int32、tf.int64、tf.unit8 ；布尔型：tf.bool ；复数型：tf.complex64、tf.complex128。

---

张量的意义

张量（Tensor）的主要使用用途：

[1] >>> 对中间结果的引用

直接计算向量和，可读性较差：

result2 = tf.constant([1.0, 2.0], name='a') + tf.constant([1.0, 2.0], name='b')

使用张量记录中间结果，增强代码可读性：

a = tf.constant([1.0, 2.0], name="a")
b = tf.constant([3.0, 4.0], name="b")
result = a + b

除了提高代码可读性，这还使得我们的计算更加方便与灵活：

# 如卷积神经网络中，我们卷积层和池化层都有可能改变张量维度，通过中间结果的引用，我们可以随时查看计算维度的变化:
print (result.shape)
# (2,)
print (result.get_shape())
# (2,)

张量还可以通过自身属性字段，查看其属性值：

print(result.name)
# add:0
print(result.dtype)
# <dtype: 'float32'>

[2] >>> 用来获取计算结果

张量本身没有存储具体数值（计算结果对我们来说是重要的），但它是对计算结果的引用。

但，我们可以通过 sess = tf.Session() ; sess.run(result) 来取得张量所对应的计算结果。

import tensorflow as tf

a = tf.constant([1.0, 2.0], dtype=tf.float32, name="a")
b = tf.constant([3.0, 4.0], dtype=tf.float32, name="b")
result = a + b

sess = tf.Session()
sess.run(result)
# array([4., 6.], dtype=float32)

可以发现，其计算结果是一个数组。

---

TF 运行模型（Session：会话）

在计算图部分我们提到过 >>>TensorFlow 程序可以分为两个阶段：1）定义计算图中所有的计算；2）执行定义好的计算（Session）。正如前面两节介绍了 TensorFlow 如何组织数据和运算。

这一小节，我们来看 TensorFlow 中的 会话（Session） 是如何来执行定义好的运算的：

• 会话用来执行计算图中定义好的运算；
• 会话拥有并管理 TensorFlow 程序运行时的所有资源；
• 计算完成后需要关闭会话来帮助系统回收资源，否则会出现资源泄漏问题。

相信，看到这里你应该明白了 TF 中会话机制存在的一部分意义了~~~

---

由于会话的使用可能导致资源泄漏问题的出现，这里衍生出了会话的两种使用模式：

两种会话使用模式

[1] >>> 明确调用会话生成函数和关闭函数

import tensorflow as tf

a = tf.constant([1.0, 2.0], dtype=tf.float32, name="a")
b = tf.constant([3.0, 4.0], dtype=tf.float32, name="b")
result = a + b

# 创建一个会话，用于执行运算：
sess = tf.Session()

# 使用创建好的会话，得到我们关心的运算结果 result ：
sess.run(result)

# 计算完成后，关闭会话回收系统资源，防止资源泄露：
sess.close()

尽管我们可以明确调用关闭函数来释放资源占用，但这种模式仍然是不安全的！！！

风险场景 >>> 当所有计算完成之后，我们需要程序明确调用 tf.Session.close() 来关闭会话并释放资源。然而，当程序因为异常而退出，导致关闭会话函数不会被执行而导致资源泄露。

基于此，TensorFlow 支持通过 Python 上下文管理器来使用会话：

[2] >>> 通过 Python 上下文管理器使用会话

# 创建一个会话，并通过 Python 上下文管理器管理这个会话：
with tf.Session() as sess:
    # 使用创建好的会话，得到我们关心的运算结果 result ：
    sess.run(result)

    # 不需要再明确调用 tf.Session.close() 函数来关闭会话了，当上下文退出时会自动关闭会话和完成资源释放。

通过 Python 上下文管理器机制，我们只需要将需要执行的运算放在 with 内部就可以。不用担心因为忘记关闭会话或程序异常退出导致的资源泄露问题。

---

默认会话机制

在计算图的使用部分，我们提到过 TensorFlow 会自动生成一个默认的计算图，如果没有特殊指定，运算会被自动加入到默认的计算图。

TensorFlow 会话也有类似的机制，但 TensorFlow 不会自动生成默认的会话，需要我们去手动指定（想想这也是合理的）。当会话被指定被指定为默认会话后，我们可以使用默认会话的一些相关函数方法：

# 当默认会话被指定后，可以通过 tf.Tensor.eval() 函数来直接获得计算结果：
sess = tf.Session()
with sess.as_default():

    print(result.eval())  # 是不是很方便
    # [4. 6.]

sess.close()

注意，以下代码也可完成相同功能：

sess = tf.Session()

# 下面两个指令功能相同：
print(sess.run(result))
# [4. 6.]
print(result.eval(session=sess))  # 并非只有在默认会话中才可以使用，但此时你需要传入会话
# [4. 6.]

sess.close()

为了交互式测试环境下更方便的使用默认会话，TensorFlow 提供了一种 交互式 下直接构建默认会话的函数：tf.InteractiveSession() ,它会自动生成会话并注册为默认会话：

sess = tf.InteractiveSession()

print(result.eval())

sess.close()

---

会话的配置

在执行会话时，我们还可以通过 ConfigProto 来配置需要生成的会话。

通过 tf.ConfigProto() 函数可以配置类似并行的线程数、GPU 分配策略、运算超时等参数，最常使用的有两个：

config = tf.ConfigProto(allow_soft_placement=True,
                        log_device_placement=True)

# 不管使用什么方式创建会话都可以进行配置：
sess1 = tf.InteractiveSession(config=config)
sess2 = tf.Session(config=config)

| ================================================== 参数说明 =============================================== |

[1] >>> allow_soft_placement: 布尔型参数

当 allow_soft_placement = True 时，在以下任意一个条件成立时，GPU 运算可以放到 CPU 上进行：

• 运算无法在 GPU 上执行（GPU 上不支持该类型数值运算）；
• 没有 GPU 资源（比如运算被指定在第二个 GPU 上运行，当机器只有第一个 GPU资源）；
• 运算输入包含对 CPU 计算结果的引用。

allow_soft_placement 参数默认为 False，但为了使得代码的移植性更强（可以同时适应 GPU 和 CPU 环境），一般会将其设置为 True。并且不同 GPU 驱动版本可能对计算的支持有略微差别，当某些运算无法被当前 GPU 支持时，可以自动调整到 CPU，而不是报错。

[2] >>> log_device_placement: 布尔型参数

当 log_device_placement = True 时，日志中会记录每个节点被安排在哪个设备上以便调试。而在生产环境将其设置为 False 可以减少日志量（如下）。

Device mapping:
add: (Add): /job:localhost/replica:0/task:0/device:CPU:0
2023-05-09 20:55:04.597829: I tensorflow/core/common_runtime/placer.cc:1059] add: (Add)/job:localhost/replica:0/task:0/device:CPU:0
a: (Const): /job:localhost/replica:0/task:0/device:CPU:0
2023-05-09 20:55:04.598370: I tensorflow/core/common_runtime/placer.cc:1059] a: (Const)/job:localhost/replica:0/task:0/device:CPU:0
b: (Const): /job:localhost/replica:0/task:0/device:CPU:0
2023-05-09 20:55:04.598836: I tensorflow/core/common_runtime/placer.cc:1059] b: (Const)/job:localhost/replica:0/task:0/device:CPU:0

---

推荐阅读！！！这里是为了快速引入神经网络（Neural Network）的 TensorFlow 实现。关于神经网络（Neural Network）更系统、全面的介绍，你可以参考博文系列【Deep Learning (深度学习) 】来进行快速学习。

这一部分，我们将简单介绍神经网络（Neural Network）的基本概念，主要计算流程，以及如何通过 TensorFlow 来实现神经网络计算。

初识神经网络

在正式开始学习神经网络之前，你必须对神经网络的基本结构 >>>> 神经元模型 有一定的了解：

神经元模型

首先我们给出人工神经网络中，神经元模型的示意图：

从上图看出，一个神经元有多个输入和一个输出。每个神经元的输入既可以是其他神经元的输出，也可以是整个神经网络的输入（非神经元节点）。

严格来说 >>>> 神经网络中除了输入层之外的所有节点都代表了一个神经元结构。

很多文档会将输入节点也看作是神经元，所以输入层有时也被看作一层神经网络层（这也是很多时候将一个只有一层隐藏层和输出层的神经网络称为三层神经网络的原因，严格来说，应该是两层神经网络结构）。

根据神经元模型可知 >>> 神经元的输出就是其所有输入的加权和以及偏置项，并通过一个激活函数得到。而不同的输入权重以及神经元节点的偏置就是神经元的参数，神经网络的优化（训练）过程就是优化（训练）神经元中参数的过程。

---

神经网络结构

所谓的神经网络结构：是指 不同神经元之间的连接方式。

本篇，我们将以 三层全连接神经网络结构（Full-Connection Neural Network，FCNN，相邻两层之间任意两个神经元节点之间都有连接）为样例解读神经网络的实现（如下图中网络结构）。

后面的博文系列中，你还会继续学习卷积神经网络（CNN）、循环神经网络（RNN）、残差神经网络等等其它经典神经网络结构。

👇👇👇 TF 游乐场以及神经网络实现流程 👇👇👇

你可以通过 TensorFlow 游乐场工具来快速认识神经网络的整体工作流程 >>>【TensorFlow 游乐场】 <<< 它是一个通过网页浏览器就可以训练的简单神经网络，并实现了可视化训练过程的工具。下图给出了 TensorFlow 游乐场工具页面示意图：

详细操作教程见网络【TensorFlow 游乐场教程】，由于篇幅原因，这里不做介绍。

---

神经网络通用流程

有了上面的认识，这里我们首先给出使用神经网络解决经典分类/回归问题的主要流程：

• 从给出的原始数据提取实体的特征向量作为神经网络的输入；
• 定义神经网络结构，以及神经网络的前向传播算法（从输入到输出）；
• 定义损失函数以及反向传播优化算法，并通过训练优化神经网络参数；
• 使用训练好的神经网络模型来预测未知数据类型；

关于输入的原始数据特征向量，取决于数据集，这里不过多介绍。先分别来看其它部分内容：

前向传播算法（FP）

简单地说，定义神经网络连接结构，以及如何从输入得到输出的过程，就是 >>> 定义神经网络的前向传播（Forward-Propagation）算法的过程（从输入到输出）。

不同结构的神经网络前向传播的方式是不相同的，但大体上是相似的。

以上面的三层全连接神经网络（FCNN）结构的前向传播算法为例进行说明 >>>>

由上图可知：神经网络前向传播算法需要三部分信息(W 上标表示神经网络层数)：

• 神经网络输入层；
• 神经网络连接结构（全连接），隐藏层 && 输出层；
• 各层神经元个数以及参数（为了简化理解，这里仅指权重，不包含偏置项，不使用激活函数）。

故，我们需要依次计算神经元节点 a_11、a_12、a_13 以及 Y 的输出结果（即神经网络如何进行前向传播！！！）。

| ================================================== Split Line =============================================== |

👇👇👇 矩阵运算表示 👇👇👇

实际上，我们可以把同属一个网络层的所有节点的计算过程表示为矩阵运算。

假设我们要求隐藏层所有节点的值 a^(1) = [a_11, a_12, a_13] 以及输出层节点的值 Y = [y]，前向传播计算过程如下：

首先表示输入的特征向量（一维数组）：

$$ x = [x_1, x_2] $$

隐藏层的权重矩阵为：

$$ W^{(1)} = \left[ \begin{array} {cccc}
W_{1,1}^{(1)} & W_{1,2}^{(1)} & W_{1,3}^{(1)}\\
W_{2,1}^{(1)} & W_{2,2}^{(1)} & W_{2,3}^{(1)}
\end{array} \right] $$

权重矩阵中的每一行元素，都表示和输入层某个节点 x_i 的全连接边上的权重（对应三条边）。

矩阵运算过程如下，展示了节点 a^(1) 的整个前传播计算过程：

$$ a^{(1)} = [a_{11}, a_{12}, a_{13}] = xW^{(1)} = [x_1, x_2]\left[ \begin{array} {cccc}
W_{1,1}^{(1)} & W_{1,2}^{(1)} & W_{1,3}^{(1)}\\
W_{2,1}^{(1)} & W_{2,2}^{(1)} & W_{2,3}^{(1)}\\
\end{array} \right] \\ = [W_{1,1}^{(1)}x_1+W_{2,1}^{(1)}x_2, W_{1,2}^{(1)}x_1+W_{2,2}^{(1)}x_2, W_{1,3}^{(1)}x_1+W_{2,3}^{(1)}x_2] $$

类似的，输出层节点的输出可以表示为：

$$ Y = [y] = a^{(1)}W^{(2)} = [a_{11}, a_{12}, a_{13}]\left[ \begin{array} {cccc} W_{1,1}^{(2)}\\ W_{2,1}^{(2)}\\ W_{3,1}^{(2)}\
\end{array} \right] = [W_{1,1}^{(2)}a_{11} + W_{2,1}^{(2)}a_{12} + W_{3,1}^{(2)}a_{13}] $$

这样，就将前向传播算法通过矩阵乘法的方式给出了~~~

不知道你发现了没有 >>>>

对于权重矩阵而言，当前网络层（Layer）每增加一个神经元节点，其权重矩阵就增加一列！！！

并且，对于多个样本数据（N）的特征向量，可以将其分别以行的形式添加到 x 样本的下面，构成（N × 2）的样本输入特征向量矩阵。最终生成（N * 2）×（2 * 3）×（3 * 1）>>>（N × 1）的结果数组。

| ================================================== Split Line =============================================== |

👇👇👇 TensorFlow 实现 👇👇👇

TensorFlow 中矩阵乘法（Matrix Multiply-ication）是很容易实现的，我们通过 TensorFlow 来表示 FCNN 的前向传播计算过程：

$$ a^{(1)} = tf.matmul(x, W^{(1)}) $$

$$ y = tf.matmul(a^{(1)}, W^{(2)}) $$

这里为了简化说明，我们简化了神经元模型中的偏置项（Bias）、激活函数（Activation-Function）等神经元结构，以及更加复杂的神经网络结构（RNN、CNN、Resnet）等的前向传播过程说明。后续博文系列中将会不断的完善，先上车后补票~~~

---

这一部分目的上是为了给出上文 FCNN 前向传播算法的 TensorFlow 具体实现。由于涉及到了 TensorFlow 变量的相关内容（内容较多），故设立一个新节进行说明，将其看作上一小节的补充即可。

TF 变量和网络参数表示

上文我们通过矩阵乘法，讲解了 FCNN 前向传播算法的实现原理，我们知道神经网络中的参数（权重）就是一个个的矩阵（数组）。

那么，TensorFlow 中如何组织以及存储神经网络中的参数？？？<<<< TF 变量 登场！！！

| ================================================== Split Line =============================================== |

TF 变量定义

TensorFlow 中提供了一个 tf.Variable(initial_value) 函数用来定义变量，来保存和更新神经网络中的参数。

和其它编程语言类似，TensorFlow 中的变量在声明时也需要指定初始值，对变量进行初始化。

TensorFlow 中变量的初始值可以设置为：

• 随机数
• 常数
• 其它变量的的初始值

下面我们将会分别介绍上述几种初始化方法：

[1] >>> 随机数生成器赋值

在神经网络中，给参数赋予随机初始值最为常见，所以一般使用随机数给 TensorFlow 中的变量进行初始化。

这里给出一个 TensorFlow 中声明一个 (2, 3) 的权重矩阵变量，并采用满足标准正态的值进行初始化的方法：

weights = tf.Variable(tf.random_normal([2, 3], stddev=2))

# tf.random_normal([2, 3], stddev=2) 函数：
# 会产生一个 Shape 为（2, 3）的矩阵，矩阵中的元素是 >>> 满足正态分布，均值为 `0`，标准差（Standard Deviation）为 `2` 的随机数。
# 参数 mean 用来指定均值（默认为 0）: `tf.random_normal([2, 3], stddev=2， mean=0)`
# random_normal() 中也支持设置随机种子 seed。

代码中调用了 TF 变量的声明函数 tf.Variable()。并且在声明函数中给出了变量的随机数初始化函数 tf.random_normal()。

↓↓↓↓↓↓ TensorFlow 中支持的几种常用随机数生成器 ↓↓↓↓↓↓

函数名称	随机分布	主要参数
tf.random_normal	正态分布	平均值、标准差、取值类型
tf.truncated_normal	截断正态分布	平均值、标准差、取值类型
tf.random_uniform	均匀分布	最小、最大取值，取值类型
tf.random_gamma	Gamma分布	形状参数 alpha、尺度参数 beta、取值类型

其中，截断正态分布表示（比较常用）：如果随机出来的值偏离平均值超过 2 个标准差，会重写随机数。

使用推荐 >>>> 随机数初始化，通常用来给神经网络的权重（Weight）参数进行初始化！！！

---

[2] >>> 常量赋值

正如前面向量加法样例中展示的，TensorFlow 中也支持通过常数来初始化 TF 变量。

TensorFlow 中支持的几种常用的常数初始化方法：

函数名称	随机分布	样例
tf.zeros	产生全为 0 的数组	tf.zeros([2,3], int32) -> [[0,0,0],[0,0,0]]
tf.ones	产生全为 1 的数组	tf.ones([2,3], int32) -> [[1,1,1],[1,1,1]]
tf.fill	产生一个全部为给定数字的数组	tf.fill([2,3],9) -> [[9,9,9],[9,9,9]])
tf.constant	产生一个给定值的常量	tf.constant([1,2,3]) -> [1,2,3]

如果你熟悉 NumPy 数组的话，对上面的用法应该不会刚到陌生。

使用推荐 >>>> 神经网络中的偏置项（Bias）通常会使用常数的形式来进行初始化！！！

biases = tf.Variable(tf.zeros([3]))
print (biases)
# <tf.Variable 'Variable:0' shape=(3,) dtype=float32_ref>

---

[3] >>> 其它变量赋值

TensorFlow 也支持通过其它变量的初始值来初始化新变量，如下：

weight1 = tf.Variable(tf.random_normal([2,3], stddev=2, dtype=tf.float32))
weight2 = tf.Variable(weight1.initialized_value())

需要注意的是 >>>> 该方法不太常用！！！

| ================================================== Split Line =============================================== |

👇👇👇 tf.Variable 操作会添加一些额外的 Op 到 Graph 👇👇👇

• 一个 Variable 操作，用于存放变量的值；
• 一个将变量设置为初始值的操作，它是一个 tf.assign 操作；
• 一个 初始化操作，例如：zeros or ones 等；
• …

你可以通过如下语句来查看当前计算图（Graph）上的所有节点：

[tensor.name for tensor in tf.get_default_graph().as_graph_def().node]

---

TF 变量的使用

上面你已经了解了 TF 变量如何声明以及初始化(事实上并没有真正被执行，仅在计算图上定义了一个计算节点)。

并且，你需要注意的是 >>>> TensorFlow 中，TF 变量在被使用之前，这个 变量初始化的过程必须被明确调用后，才可以使用！！！否则报错：

Attempting to use uninitialized value XXXX

如何理解？！！来看一个矩阵乘法样例：

>>> import tensorflow as tf

# 这里输入必须是二维的（1, 2），否则无法进行矩阵乘法运算：
>>> x = tf.constant([[1, 2]], dtype=tf.float32)
>>> w = tf.Variable(tf.random_normal([2, 3], stddev=1))
>>> y = tf.matmul(x, w)

>>> sess = tf.InteractiveSession()
>>> sess.run(y)
# 这里会产生变量未初始化报错：Attempting to use uninitialized value XXXX
# 这是由于在计算 y 时，会使用到 TF 变量 `w`，其未明确的进行初始化调用！！！

故，TF 变量使用前必须要明确进行初始化的调用( sess.run(w_TF_Variable.initializer) )：

# 明确进行初始化调用：
>>> sess.run(w.initializer)

>>> sess.run(y)
array([[-0.17434047, -3.660441  ,  1.0128452 ]], dtype=float32)
>>> sess.close()

| ================================================== Split Line =============================================== |

👇👇👇 引发的一个问题 👇👇👇

上面的样例中，我们在使用变量 w 之前需要明确调用其初始化，完成最终的初始化。

虽然这看上去是一个可行的方案，但你有没有想过：当我们的模神经网络的变量数目增多（通常会有几万，甚至几十、几百万的参数），或者变量之间存在依赖关系时，你还会去一个个的为每个变量做明确初始化调用么？当然不会！！！太麻烦了~~~

TensorFlow 提供了一种更便捷的方法来一步完成所有变量的初始化调用。如下所示：

# New Version:
init_op = tf.global_variables_initializer().run()

# 你可能还会看见这样的表达：
init_op = tf.initializer_all_variables().run()
# Old Version（新版本下会报错，已弃用）：
---------------------------------------------------------------------------
AttributeError                            Traceback (most recent call last)
<ipython-input-75-2501d5753001> in <module>()
        1 # Old Version(新版本下会报错)：
----> 2 init_op = tf.initializer_all_variables().run()
AttributeError: module 'tensorflow' has no attribute 'initializer_all_variables'

---

TF 变量属性

类似张量（Tensor），维度（shape）和类型（dtype）也是变量最重要的两个属性。

👇👇👇 [1] >>> 类型（dtype） 👇👇👇

类似于强类型语言，一个变量一旦构建之后，变量的类型就不能再改变。

如上面给出的前向传播样例中，w 类型为 tf.random_normal 函数结果的默认类型 tf.float32，那么它就不能被赋予其它类型的值，如下代码所示：

w1 = tf.Variable(tf.random_normal([2,3], stddev=1, name="w1"))
w2 = tf.Variable(tf.random_normal([2,3], dtype=tf.float64, stddev=1, name="w2"))

# w2 赋值给 w1：
tf.assign(w1, w2)  # 等同于下面
# w1.assign(w2)

执行上述程序语句将报错：TypeError: Input 'value' of 'Assign' Op has type float64 that does not match type float32 of argument 'ref'。

这类似于张量，TensorFlow 会自动对变量的类型进行类型检查！！！

| ================================================== Split Line =============================================== |

👇👇👇 [2] >>> 维度（shape） 👇👇👇

维度是变量另外一个重要的属性。和类型不大一致，维度在 TF 程序中是可变的，但需要通过参数 validate_shape=False（固定形状）设置。

如下样例：

>>> import tensorflow as tf

>>> w1 = tf.Variable(tf.random_normal([2,3], stddev=1, name="w1"))
>>> w2 = tf.Variable(tf.random_normal([2,2], stddev=1, name="w2"))

# tf.assigh(w1,w2)
# ValueError: Shape (2,3) and (2,2) are not compatible

# 这样才可以执行：
>>> tf.assign(w1,w2, validate_shape=False)
<tf.Tensor 'Assign:0' shape=(2, 2) dtype=float32_ref>

当然，TensorFlow 支持改变变量维度的用法在实践中比较罕见。

| ================================================== Split Line =============================================== |

👇👇👇 [3] >>> trainable && collections 👇👇👇

计算图中提到过，TensorFLow 中可以通过集合（Collection）来管理运行时的各种资源，并且它自动维护一些默认集合。

例如，所有的变量都会被自动加入到 tf.GraphKeys.VARIABLES/ 集合，你可以通过 tf.all_variables() 函数可以拿到当前计算图上所有的变量以便 TF 持久化TensorFlow 整个计算图的运行状态

tf.Variable() 变量有一个 collections 属性可用于指定新变量所属的集合，默认为 [GraphKeys.GLOBAL_VARIABLES]，支持指定新的集合（例如 loss）。

另外，当构建机器学习模型时，我们需要不断优化参数以获得最佳的模型，可以通过变量声明函数中的 trainable 属性来区分需要优化的参数（神经网络中的参数）和其他参数（迭代轮数）：

如果声明变量时参数 `trainable` 为 `True`（默认），那么这个变量会被加入到 `tf.GraphKeys.TRAINABLE_VARIABLES` 集合。

你可以在 TF 中可以通过 tf.trainable_variables() 函数得到所有需要优化的参数。并且 TensorFlow 中提供的神经网络优化算法会将 tf.GraphKeys.TRAINABLE_VARIABLES 集合中的变量作为默认的优化对象。

---

Variables VS Tensor

前面，我们提到：TensorFlow 中所有的数据都是通过 Tensor 来组织和管理的，这一小节我们又介绍了通过 TensorFlow 变量来保存和更新参数。

那么，张量和变量是什么关系呢？！！

TensorFlow 中，变量（Variables）的声明函数是一个运算，而张量（Tensor）是对运算结果的引用个。

所以不难看出，这个张量就是我们这一小节所说的变量，也就是说 变量是一种特殊的张量。

---

TF 实现前向传播算法

结合上面的知识储备，我们给出 FCNN 的前向前向传播算法的 TensorFlow 实现：

import tensorflow as tf

# 定义一个变量用于作为神经网络输入，暂时将输入特征向量(即一个样本的特征向量)定义为一个常量(1 * 2 的矩阵)：
input_x = tf.constant([[0.7,0.9]], dtype=tf.float32)

# 声明两个权重变量：w1、w2（这里还通过 seed 设置了随机种子，可以保证每次运行得到的结果一样）
w1 = tf.Variable(tf.random_normal([2, 3], stddev=1, seed=1))
w2 = tf.Variable(tf.random_normal([3, 1], stddev=1, seed=1))

# 通过前向传播算法原理获得神经网络的输出 Y：
a = tf.matmul(input_x, w1)
y = tf.matmul(a, w2)

# 创建会话来执行定义好的运算：
sess = tf.Session()

# 使用变量 w1、w2 之前,需要明确调用变量的初始化才可以使用：
sess.run(tf.global_variables_initializer())

# 执行运算，获取最终结果：
print (sess.run(y))

sess.close() # 关闭会话，释放资源

样例结果输出：[[3.957578]]。

---

神经网络模型优化

上面我们给出了一个样例来完成 FCNN 的前向传播过程。但是，这个样例中所有变量（参数）的初始取值都是随机的。

事实上，在使用神经网络来解决实际的分类/回归问题时，我们需要 >>>> 使用样本数据，不断训练神经网络模型优化模型参数（不断拟合数据集，发现其潜在规律），以获取到更好的参数取值，以获取最佳的神经网络模型。

这一小节将介绍如何使用监督学习（Supervised Learning）的方式，并且结合训练算法（反向传播算法，Back Propagation，BP）来更合理的设置参数取值。

优化神经网络中参数的过程，就是神经网络的训练过程，只有经过有效训练的神经网络模型才可以真正解决分类/回归问题。

监督学习最重要的思想 就是 >>>> 在已知答案（标签，Label）的标注数据集上，使模型给出的预测结果要尽可能接近真实标记。通过 BP 算法调整神经网络中的参数对训练数据的拟合，可以使得模型对未知样本提供预测能力。

---

反向传播算法（BP）

在神经网络优化算法中，最常用的方法就是反向传播算法（BP）。这里，我们先简单了解一下反向传播算法（Back Propagation，BP）的概念，后续会做深入介绍。

BP 是训练神经网络的核心算法，它可以 >>> 根据定义好的损失函数（Loss Function）来不断迭代优化神经网络中参数的取值，从而使得神经网络模型在训练数据集上的损失函数达到一个较小值。反向传播算法训练神经网络模型的流程图（迭代过程）：

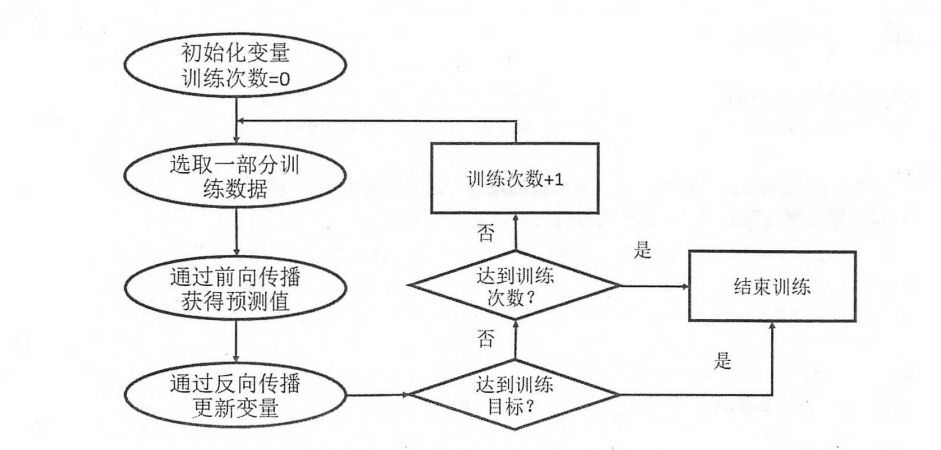
如图可见，反向传播算法本质是实现了一个迭代的过程。

↓↓↓↓↓↓ 训练第一阶段：FP ↓↓↓↓↓↓

每次迭代开始，首先需要读取一部分训练数据（来源于训练数据集），这一小部分数据称为一个 batch。然后这个 batch 的数据通过前向传播算法得到其在神经网络模型的预测结果。

↓↓↓↓↓↓ 训练第二阶段：BP ↓↓↓↓↓↓

此时，由于训练数据都是有正确答案标注（Label）的，所有可以计算出当前神经网络模型的预测答案和正确答案的差距（通过损失函数来定义）。最后，反向传播算法会根据这个差距更新神经网络的参数，使得预测结果要尽可能接近真实标记。

可见，反向传播算法核心：计算 Loss && 更新参数。

---

TF占位符和 Batch 表达

TF 实现反向传播算法之前，我们需要了解一下 TF 如何从训练数据集读取一个 batch 的数据，在 TensorFlow 中进行表达。

前面，我们在实现 FCNN 的前向传播算法样例中，曾经使用过用常量来表达一个样本数据：

input_x = tf.constant([[0.7,0.9]], dtype=tf.float32)

↓↓↓↓↓↓ 引发一个问题 ↓↓↓↓↓↓

如果每次迭代中选取的数据都要通过常量来创建，那么 TensorFlow 的计算图将会太大。

因为每生成一个常量，TensorFlow 都会在计算图中增加一个计算节点。一般来说，一个神经网络的训练过程会经过几百万轮甚至几亿轮数的迭代，这样计算图就会非常大，而且利用率很低。

👇👇👇 解决办法 👇👇👇

为了避免这个问题，TensorFlow 提供了一个占位符机制（placeholder）用于提供输入数据。placeholder 相当于定义了一个位置（占位），这个位置中的数据在程序运行时再指定（必须），运行时只需要将读入的数据通过 placeholder 传入 TF 计算图即可。

也就是说，我们通过 placeholder 告诉 TF 程序，这里有一个“空间”，我们会在执行程序时再给定这个 “空间” 的取值以供计算图使用。

---

[1] >>> placeholder 占位符

先来给出占位符的函数形式：

tf.placeholder(dtype, shape=None, name=None)

占位符中，数据类型（dtype）是需要指定的，而且和其它张量一样，类型是不可更改的；维度信息可以根据提供的数据自动推导得出，所以不一定要给出。

这里，给出将 placeholder 引入全连接神经网络的前向传播算法实现中的样例：

import tensorflow as tf

# placeholder 的使用：
input_x = tf.placeholder(tf.float32, shape=(1, 2), name="input_x")

# 声明两个权重变量：w1、w2（这里还通过 seed 设置了随机种子，可以保证每次运行得到的结果一样）
w1 = tf.Variable(tf.random_normal([2, 3], stddev=1, seed=1))
w2 = tf.Variable(tf.random_normal([3, 1], stddev=1, seed=1))

# 通过前向传播算法原理获得神经网络的输出 Y：
a = tf.matmul(input_x, w1)
y = tf.matmul(a, w2)

# 创建会话来执行定义好的运算：
sess = tf.Session()

# 使用变量 w1、w2 之前,需要明确调用变量的初始化才可以使用：
sess.run(tf.global_variables_initializer())

# 执行运算，获取最终结果：
print (sess.run(y))

sess.close() # 关闭会话，释放资源

我们发现，直接执行 sess.run(y) 会发生报错： InvalidArgumentError (see above for traceback): You must feed a value for placeholder tensor 'input_x_1' with dtype float and shape [1,2]。

WTF ？？？

---

哦，想到了：占位之后，在程序运行时必须为 “占位空间” 传入数据值~~~

上面仅仅是在计算图中创建了一个占位符，但是运行时（sess.run(y)）我们并没有给 placeholder 传入数据。

[2] >>> 神奇的 feed_dict

TensorFlow 中可以使用 feed_dict（feed 字典）来为运行时的 placeholder 空间 feed（喂养）样本数据，feed_dict 字典中需要给出每个用到的 placeholder 取值（一个 batch 的数据）。

实例代码如下：

import tensorflow as tf

# placeholder 的使用（定义了一个（3, 2）的空间）：
input_x = tf.placeholder(tf.float32, shape=(3,2), name="input")

# 声明两个权重变量：w1、w2（这里还通过 seed 设置了随机种子，可以保证每次运行得到的结果一样）
w1 = tf.Variable(tf.random_normal([2,3], stddev=1, seed=1))
w2 = tf.Variable(tf.random_normal([3,1], stddev=1, seed=1))

# 通过前向传播算法原理获得神经网络的输出 Y：
a = tf.matmul(input_x, w1)
y = tf.matmul(a, w2)

# 创建会话来执行定义好的运算：
sess = tf.Session()

# 明确调用变量
init_op = sess.run(tf.global_variables_initializer())

# 执行运算会报错：
# print (sess.run(y))
# batch 中含有 3 个样本（当然可以包含多个）：
print (sess.run(y, feed_dict={input_x: [[0.7,0.9], [0.1,0.4], [0.5,0.8]]}))

sess.close() # 关闭会话，释放资源

样例运行结果如下（每一行都是一个样本的前向传播结果）：

[[3.957578 ]
 [1.1537654]
 [3.1674924]]

---

Loss Function && Optimizer

前面说过，反向传播算法实现的核心：

• 计算 Loss：通过定义损失函数，计算当前神经网络模型的预测答案和正确（期望）答案的差距；
• 更新参数：向着预测和期望差距更小的方向（Loss 更小），更新神经网络的参数。

也就是说 >>>> BP 实现需要 >>>>

[1] >>> 定义一个合适损失函数（Loss Function）来刻画当前预测值和期望值之间的差距；

[2] >>> 然后通过合适的参数优化器（Optimizer）来调整神经网络参数取值使得差距逐渐被缩小。

下面我们给出一个简单的反向传播算法模型的定义：

# 定义交叉熵损失函数：
cross_entropy = -tf.reduce_mean(y_ * tf.log(tf.clip_by_value(y, 1e-10, 1.0)))

# 定义反向传播算法的优化器（Ada）：
train_op = tf.train.AdamOptimizer(learning_rate).minimize(cross_entropy)

除了定义合适的损失函数外，我们还需要根据实际问题采用合理的反向传播优化器以更新参数（更新参数对我们来说是关键的）。TF 中支持的三种常用优化器：tf.train.GradientDescentOptimizer()、tf.train.AdamOptimier()、tf.train.MomentumOptimizer()。

这里关于损失函数和反向传播算法优化器的选择，你不用深究，下一篇博文会给出如何针对特定的问题选择合适的 Loss Function && Optimizer。

| ================================================== Split Line =============================================== |

👇👇👇 如何执行反向传播算法 👇👇👇

上面在定义了 BP 之后，直接通过运行 sess.run(train_op) 就可以对所有在 tf.GraphKeys_TRAINABLE_VARIABLES() 集合中的变量进行自动优化，使得神经网络模型在当前 batch 的损失函数更小。

---

TF 实现的 FCNN 模型优化实例

综上所述，这一小节我们将在一个模拟数据集上训练全连接神经网络模型来解决经典的二分类问题。

由于没有数据集，这里我们使用了 Numpy 随机模块模拟了一个带标签的包含 128 个样本数据的训练数据集。

完整实例代码如下：

### TF 实现的 FCNN 模型优化实例 ###
import tensorflow as tf

from numpy.random import RandomState

# 定义训练数据 batch 的大小
batch_size = 8

# 待输入的样本特征向量以及标注的占位符：
# Shape 设置 None 方便自适应不同的 batch 大小
input_x = tf.placeholder(dtype=tf.float32, shape=(None, 2), name="input_x")
input_y = tf.placeholder(dtype=tf.float32, shape=(None, 1), name="input_y")

# 定义全连接神经网络的参数
w1 = tf.Variable(tf.random_normal([2, 3], stddev=1, seed=1))
w2 = tf.Variable(tf.random_normal([3, 1], stddev=1, seed=1))

# 定义神经网络的前向传播：
a = tf.matmul(input_x, w1)
y = tf.matmul(a, w2)

# 定义神经网络模型的反向传播算法：
# 1）定义损失函数：
cross_entropy = -tf.reduce_mean(input_y * tf.log(tf.clip_by_value(y, 1e-10, 1.0)))
# 2）定义反向传播的优化器：
learning_rate = 0.001
train_op = tf.train.AdamOptimizer(learning_rate).minimize(cross_entropy)

# 通过随机数生成一个模拟数据集：
rdm = RandomState(1)
dataset_size = 128 # 训练数据集样本数目
X = rdm.rand(dataset_size, 2)
# 定义规则给出样本的标签（x1+x2<1 认为是正样本）：
Y = [ [int(x1+x2 < 1)] for (x1, x2) in X ]

# 下面创建一个会话来运行程序：
with tf.Session() as sess:
    
    # 明确调用变量初始化：
    init_op = sess.run(tf.global_variables_initializer())
    # 打印训练之前的神经网络参数：
    print("| ============= Parameters Before Training ============ |")
    print("Weight1 >>>", "\r\n", sess.run(w1))
    print("Weight2 >>>", "\r\n", sess.run(w2))
    print("| ===================================================== |")
    
    # 开始训练：
    # 定义训练轮数：
    STEPS = 5000
    
    for i in range(STEPS):
        # 每次选取一个 batch 的数据进行训练：
        start = (i * batch_size) % dataset_size
        end = min(start + batch_size, dataset_size)
        
        # 够着 feed dict，用于给 placeholder 传入数据：
        data_feed = feed_dict = {input_x: X[start:end], input_y: Y[start:end]}
        
        # 训练神经网络参数
        sess.run(train_op, data_feed)
        
        # 每迭代 1000 次输出一次在所有数据上的交叉熵损失：
        if i % 1000 == 0:
            total_cross_entropy = sess.run(cross_entropy, feed_dict={input_x: X, input_y:Y})
            print ("After %d training step(s), cross entropy on all data is %g" % (i, total_cross_entropy))
            
    # 打印训练之后的神经网络参数：
    print("| ============= Parameters After Training ============ |")
    print("Weight1 >>>", "\r\n", sess.run(w1))
    print("Weight2 >>>", "\r\n", sess.run(w2))
    print("| ===================================================== |")

样例程序输出日志信息如下：

| ============= Parameters Before Training ============ |
Weight1 >>> 
 [[-0.8113182   1.4845988   0.06532937]
 [-2.4427042   0.0992484   0.5912243 ]]
Weight2 >>> 
 [[-0.8113182 ]
 [ 1.4845988 ]
 [ 0.06532937]]
| ===================================================== |
After 0 training step(s), cross entropy on all data is 0.0674925
After 1000 training step(s), cross entropy on all data is 0.0163385
After 2000 training step(s), cross entropy on all data is 0.00907547
After 3000 training step(s), cross entropy on all data is 0.00714436
After 4000 training step(s), cross entropy on all data is 0.00578471
| ============= Parameters After Training ============ |
Weight1 >>> 
 [[-1.9618274  2.582354   1.6820377]
 [-3.4681718  1.0698233  2.11789  ]]
Weight2 >>> 
 [[-1.8247149]
 [ 2.6854665]
 [ 1.418195 ]]
| ===================================================== |

可见，随着训练迭代的过程，FCNN 模型在所有数据上的交叉熵损失是逐步降低的~~~

也就也意味着，随着 FCNN 的训练，模型越来越拟合数据集。

---