TensorFlow 入门之 MNIST 手写体数字识别问题

本篇我们将针对实际中的图像识别问题，使用深度学习入门级 MNIST 手写体数字识别数据集，并且结合上一篇博文中给出的更合理的神经网络设计与优化方法，给出一个使用 TF 实现 MNIST 手写体数字识别神经网络模型优化的最佳实践。

配置过程中参考了网络上很多的相关博文，也遇到过很多坑，为了感谢配置过程中各位大佬的帮助以及方便本人下次配置或者升级，整理以作此文。

更多 TensorFlow 框架学习相关内容，请关注博主相关博文系列 ↓↓↓↓↓

之一 >>>> 一文详解全平台 TensorFlow 深度学习框架在线搭建 (CPU&GPU 支持)

之二 >>>> TensorFlow GPU 支持: Ubuntu16.04 + Nvidia GTX + CUDA + CUDNN

之三 >>>> TensorFlow 入门之 TF 基本工作原理

之四 >>>> TensorFlow 入门之深度学习和深层神经网络

之五 >>>> TensorFlow 入门之 MNIST 手写体数字识别问题

之六 >>>> TensorFlow 入门之图像识别和卷积神经网络（CNN）

---

提纲

本篇，我们总共安排了三个章节来进行学习：

[1] >>>> 简单介绍 MNIST 手写体数字图像识别数据集，并给出 TensorFlow 程序如何处理 MNIST 数据集中数据的说明；

[2] >>>> 基于 MNIST 手写体数字图像识别问题，TF 实现上一篇博文中给出的更合理的神经网络设计与优化方法，以从实际问题角度展示不同优化方法带来的模型性能提升；

[3] >>>> 通过 TF 变量命名空间，来解决 TensorFlow 变量重用的问题，最终给出 MNIST 识别问题的完整样例。

---

初识 MNIST 数据集

MNIST（Mixed National Institute of Standards and Technology Database）是一个非常有名的手写体数字图像识别数据集（NIST 数据集的一个子集），也是一个入门级的计算机视觉数据集（很多资料会将其作为深度学习入门样例）。就好比编程入门有 Hello World，机器学习入门有 MNIST。

MNIST 数据集中包含各种手写的数字图片：

MNIST 官方数据集可以分成两部分：

• 60000 行的训练数据集（mnist.train）
• 10000 行的测试数据集（mnist.test）

其中，每一行 MNIST 数据单元（数据对象）由两部分组成：一张包含手写数字的图片，和手写数字图片所对应的标签。

---

MNIST 数据单元

手写数字图像 >>>> 每一张图片都代表了一个手写的 0~9 中数字的灰度图（单通道图像），图片大小为 28 px × 28px。

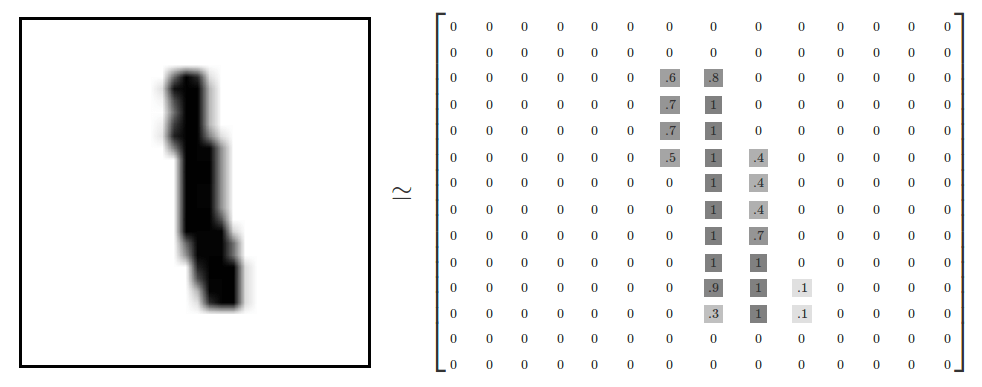
我们可以用一个像素矩阵来表示手写数字 1 的图片：

关于图像的像素矩阵表示方法，可参考文档【 >>>> The Pixel Matrix Representation Of Image <<<<】。

图像标签 >>>> 每一个手写体数字图片，都对应 0~9 中的任意一个数字。

虽然 MNIST 数据集中只提供了训练数据（训练集）和测试数据（测试集），但是为了验证模型训练时的效果，使用时一般会从训练数据集中划分出一部分数据作为验证数据（集验证集）。

---

TensorFlow Support

为了在 TensorFlow 中使用方便，TF 对 MNIST 数据集进行了内部封装，提供了一个示例模块来处理 MNIST 数据集。

# 这个模块会自动下载并转换 MNIST 数据格式，将其从原始的数据包中解析成训练和测试神经网络时可以使用的数据格式。
tensorflow.examples.tutorials.mnist

TF MNIST 数据集使用样例：

# 导入用于下载和读取 MNIST 数据集的模块:
from tensorflow.examples.tutorials.mnist import input_data

# 指定 MNIST 数据集的下载和读取的路径：
MNIST_data_Path = "./MNIST_data/"

# 获取 MNIST 数据集对象
mnist = input_data.read_data_sets(MNIST_data_Path, one_hot=True)

# print mnist.train dataSet size :
print("Training data size : ", mnist.train.num_examples)
# print mnist.validation dataSet size :
print("Validating data size : ", mnist.validation.num_examples)
# print mnist.test dataSet size :
print("Testing data size : ", mnist.test.num_examples)

# print mnist.train.images[0] / mnist.train.labels[0] Format
print("Example training data（image）: ", "\n", mnist.train.images[0])
print("Example training data lable : ", mnist.train.labels[0])

可能由于网络原因导致 MNIST 数据集下载失败，你可以参考 【 >>>> MNIST Introduction <<<<】进行手动下载！！！

下载成功后，样例程序输出结果如下：

Successfully downloaded train-images-idx3-ubyte.gz 9912422 bytes.
Extracting ./MNIST_data/train-images-idx3-ubyte.gz
Successfully downloaded train-labels-idx1-ubyte.gz 28881 bytes.
Extracting ./MNIST_data/train-labels-idx1-ubyte.gz
Successfully downloaded t10k-images-idx3-ubyte.gz 1648877 bytes.
Extracting ./MNIST_data/t10k-images-idx3-ubyte.gz
Successfully downloaded t10k-labels-idx1-ubyte.gz 4542 bytes.
Extracting ./MNIST_data/t10k-labels-idx1-ubyte.gz
Training data size :  55000
Validating data size :  5000
Testing data size :  10000
Example training data :  
 [0.         0.         0.         0.         0.         0.
 0.         0.         0.         0.         0.         0.
 1.         .................
 0.         0.         0.         0.         0.         0.
 
 0.         0.         0.         0.34901962 0.9843138  0.9450981
 0.3372549  0.         0.         0.         0.         0.
 0.         0.         0.         0.         0.         0.
 0.         0.         0.         0.         0.         0.
 0.         0.         0.         0.         0.         0.
 0.01960784 0.8078432  0.96470594 0.6156863  0.         0.
 0.         0.         0.         0.         0.         0.
 0.         0.         0.         0.         0.         0.
 0.         0.         0.         0.         0.         0.
 1.         ......................
 0.         0.         0.         0.         0.01568628 0.45882356
 0.27058825 0.         0.         0.         0.         0.
 0.         0.         0.         0.         0.         0.
 0.         0.         0.         0.        ]
Example training data lable :  [0. 0. 0. 0. 0. 0. 0. 1. 0. 0.]

👇👇👇 MNIST 数据集划分 👇👇👇

可以看出，input_data.read_data_sets 函数生成的数据集对象会自动将 MNIST 数据集划分为 train && validation && test 三个数据集。

其中，train 数据集中包含 55000 张训练图片，validation 数据集中包含 5000 张验证图片，它们共同构成了 MNIST 自身提供的训练数据集。test 数据集中包含了 10000 张测试图片，这些图片都来自于 MNIST 提供的测试数据集。

| ================================================== Split Line =============================================== |

👇👇👇 图像输入和标签处理 👇👇👇

FCNN 神经网络结构的输入是一个特征向量，所以这里需要将一张二维图像的像素矩阵扁平化处理为一维数组，方便 TF 将图片的像素矩阵提供给神经网络的输入层。

故，TF 封装模块处理后的每张手写数字图片都是一个长度为 784 的一维数组，这个数组中的元素对应了图片像素矩阵中的任意像素值（28 * 28 = 784）。为了方便计算，像素矩阵中像素的灰度值被归一化到 [0, 1]，它代表了颜色的深浅。其中 0 表示白色背景（background），1 表示黑色前景（foreground）。

并且，对手写数字图片所对应的标签，进行了 one-hot 编码处理，方便神经网络的分类任务。one-hot 标签数组是一个 10 维（长度为 10）的向量，每一个维度都对应了 0~9 中数字中的一个。形如：[0,1,0,0,0,0,0,0,0,0] <<<< 数字 1。

| ================================================== Split Line =============================================== |

👇👇👇 Mini Batch 支持 👇👇👇

为了方便使用小批量样本梯度下降（MGD），input_data.read_data_sets 函数生成的数据集对象还提供了 mnist.train.next_batch 方法，可以快速从所有的训练数据中读取一小部分数据作为一个训练 batch。

以下代码显示如何使用这个功能：

# 取 BATCH SIZE 为 100 大小的训练数据：
BATCH_SIZE = 100

xs, ys = mnist.train.next_batch(BATCH_SIZE)

print ('X Shape: ', xs.shape)  # X Shape:  (100, 784)
print ('Y Shape: ', ys.shape)  # Y Shape:  (100, 10)

关于 MNIST 数据集更加详细的说明以及使用，请参见文档【 >>>> MNIST Introduction <<<<】。

---

MNIST FCNN 模型训练以及不同优化效果对比

这一章节，首先基于 MNIST 手写体数字图像识别问题给出一个 TF 实现，这个程序整合了上一篇博文中介绍的所有优化方法。

接着，介绍验证/测试数据集在神经网络训练过程中的作用。通过实验数据来证明，神经网络在验证数据集上的表现可以近似地作为评价不同神经网络模型效果的标准或者作为迭代轮数的依据。

最后，通过模型在测试集上的表现对比上一篇博文中提到的神经网络结构设计和参数优化的不同方法，从实际问题中展示不同优化方法所带来的性能提升。

---

TF 实现 MNIST 图像识别问题

这个程序整合了上一篇博文中介绍的所有优化方法：

在神经网络结构设计上采用全连接结构，引入隐藏层、激活函数、偏置项；在训练神经网络上，引入设置指数衰减学习率、正则化以及滑动平均模型。

训练好的神经网络模型在 MNIST 测试数据集上可以达到 98.4% 左右的准确率。

完整的代码如下：

'''
  Hello TensorFlow : MNIST 手写体数字图片识别
  Neural Network Structure : Full Connection
'''
import time
from datetime import timedelta

import warnings
warnings.filterwarnings('ignore')
# import os
# os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'

import tensorflow as tf
tf.compat.v1.logging.set_verbosity(tf.compat.v1.logging.ERROR)  # 忽略 TensorFlow 警告信息

# 导入用于下载和读取 MNIST 数据集的模块
from tensorflow.examples.tutorials.mnist import input_data

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline


###################### Part 1 : Macros Variables Define ######################
## 1. MNIST 数据集相关的常数 ##

# 图像像素（28px * 28px 像素矩阵转化），输入层的节点数；
INPUT_NODE = 784
# 输出节点数，等于类别数目。分别对应 `0~9` 10 个数字类别；
OUTPUT_NODE = 10

## 2. 配置神经网络中的参数 ##

# Layes1: 隐藏层节点数，这里设置只有一层隐藏层（hidden layers）的网络结构
LAYER1_NODE = 200

# 设置滑动平均衰减率
MOVING_AVERAGE_DECAY = 0.99

# 设置描述模型复杂度（结构风险）的正则化项在损失函数中的系数(lambda)
REGULARIZATION_RATE = 0.0001

# 设置初始学习率
LEARNING_RATE_BASE = 0.8
# 设置学习率的衰减率
LEARNING_RATE_DECAY = 0.96

# 设置训练轮数
TRAINING_STEPS = 30000

# 一个训练 batch 块中的训练数据个数。
# batch 数值越小，训练过程越接近随机梯度下降；数值越大，训练越接近梯度下降。
BATCH_SIZE = 100


###################### Part 2 : Referenced Function Define #####################

'''### [1] get_time_dif：时间函数

    用于获取程序中某些功能模块所使用的时间（Seconds）

'''
def get_time_dif(start_time):
    end_time = time.time()
    time_diff = end_time - start_time
    return timedelta(seconds=time_diff)


''' ### [2] inference : 通过给定的 FCNN 输入和所有参数，计算 FCNN FP 的结果 ## 

	定义了一个带 ReLU（非线性） 激活函数的三层全连接神经网络，实现了多层网络结构以及去线性化。同时，支持：传入
用于计算参数滑动平均值的类，方便在测试时使用滑动平均模型。

'''
def inference(input_tensor, avg_class, weights1, biases1, weights2, biases2):
    # 当没有提供滑动平均类时，直接使用参数当前的取值
    if avg_class == None:
        # 计算隐藏层的 FP 结果，激活函数为 ReLU:
        layer1 = tf.nn.relu(tf.matmul(input_tensor, weights1) + biases1)
        return tf.matmul(layer1, weights2) + biases2
    else:
        layer1 = tf.nn.relu(tf.matmul(input_tensor, avg_class.average(weights1)) + avg_class.average(biases1))
        return tf.matmul(layer1, avg_class.average(weights2)) + avg_class.average(biases2)


''' ### [3] train : 模型训练 ## 

    FCNN 模型训练需要的前向传播算法、反向传播算法，以及迭代训练的实现。

'''
def train(mnist):

    x = tf.placeholder(dtype=tf.float32, shape=(None, INPUT_NODE), name="input_x")
    y_ = tf.placeholder(dtype=tf.float32, shape=(None, OUTPUT_NODE), name="input_y")
    
    # 隐藏层参数(Second layer)：
    weights1 = tf.Variable(tf.random_normal([INPUT_NODE, LAYER1_NODE], stddev=0.1, dtype=tf.float32))
    biases1 = tf.Variable(tf.constant(0.1, shape=[LAYER1_NODE]))
    
    # 输出层参数(Third layer)：
    weights2 = tf.Variable(tf.random_normal([LAYER1_NODE, OUTPUT_NODE], stddev=0.1, dtype=tf.float32))
    biases2 = tf.Variable(tf.constant(0.1, shape=[OUTPUT_NODE]))
    
    #### 1. 前向传播（FP） ####
    # 计算当前参数下 FCNN FP 的结果，模型训练时前向传播计算的 avg_class = None，所以不会使用参数的滑动平均值进行计算
    y = inference(x, None, weights1, biases1, weights2, biases2)
    
    # 定义训练时的全局步数，该变量无需计算滑动平均值。所以一般需要指定全局步数变量为不可训练变量(trainable=False)
    global_step = tf.Variable(0, trainable=False)
    #### =============== ####
    
    #### 2. 滑动平均设置 ####
    # avg_class = variable_averages
    variable_averages = tf.train.ExponentialMovingAverage(MOVING_AVERAGE_DECAY, global_step)  #  初始化滑动平均对象
    
    # 计算所有可训练神经网络参数变量的滑动平均值（即添加/更新参数变量的影子变量）：
    variables_averages_op = variable_averages.apply(tf.trainable_variables())
    # tf.trainable_variables 可返回 GraphKeys.TRAINABLE_VARIABLES 集合中所有元素（即未指定 trainable=False 的变量）
    
    # 计算使用了滑动平均之后的 FP 结果。滑动平均之后不会改变变量本身取值，会维护一个 shadow_variable 来记录其滑动平均值
    movingAvg_y = inference(x, variable_averages, weights1, biases1, weights2, biases2)
    #### =============== ####
    
    #### 3. Loss Function ####
    # 定义交叉熵损失函数（经验风险）:该函数第二个参数需要提供的是正确标签的数字，tf.argmax(y_, 1)可以获取 y_ 对应的类别标签（原型: tf.argmax(array, axis)）
    # 注意，这里的 logits 参数值只能是不使用滑动平均的变量，不能是影子变量：
    cross_entropy = tf.nn.sparse_softmax_cross_entropy_with_logits(logits=y, labels=tf.argmax(y_, 1))
    # 计算当前 batch 中所有样例的交叉熵平均值
    cross_entropy_mean = tf.reduce_mean(cross_entropy)
    
    # 定义 L2 正则化损失函数（结构风险）：
    regularizer = tf.contrib.layers.l2_regularizer(REGULARIZATION_RATE)
    # 计算模型的 L2 正则化损失（一般只计算权重的正则化损失，而不使用偏置项）:
    parm_regularization = regularizer(weights1) + regularizer(weights2)
    
    # 计算最终 Loss Function：经验风险和结构分析
    loss = cross_entropy_mean + parm_regularization
    #### =============== ####
    
    #### 4. 反向传播（BP） ####
    # 设置指数衰减的学习率:随着迭代进行，更新变量的学习率在这个基础上递减
    learning_rate = tf.train.exponential_decay(learning_rate = LEARNING_RATE_BASE,  # 初始学习率
                                               global_step = global_step,  # 训练时的全局步数
                                               decay_steps = mnist.train.num_examples / BATCH_SIZE,  # 遍历一次所有训练数据需要的迭代次数
                                               decay_rate = LEARNING_RATE_DECAY  # 衰减系数
                                              )
    # 优化器:
    train_step = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss, global_step=global_step)
    
    # 绑定参数滑动平均计算和参数梯度更新计算
    # 每迭代一次数据就需要通过 BP 来更新 FCNN 中参数，又要更新每一个参数的滑动平均值（影子变量）。
    # TF 中提供了两种机制：tf.control_dependencie 和 tf.group：
    # # train_op = tf.group(train_step, variables_averages_op) # 等价于 ==
    with tf.control_dependencies([train_step, variables_averages_op]):
        train_op = tf.no_op(name='train')
    #### =============== ####

    ## 5. Model Evaluation ##
    # 检验使用了滑动平均模型的 FCNN 模型的效果（滑动平均或不使用滑动平均）
    # correct_prediction = tf.equal(tf.argmax(movingAvg_y, 1), tf.argmax(y_, 1))
    correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(y_, 1))
    # tf.cast(x, dtype) 会将 x 数据格式转化成 dtype 数据格式。这里，将 bool 型数值转为 float 后，x 会变为 0/1 序列。
    # 计算模型准确率
    accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
    
    
    ############################  Begin To Training  ###########################
    
    # 定义会话配置:
    config = tf.ConfigProto(# device_count={"CPU": 4}, # limit to num_cpu_cor CPU usage
                            # inter_op_parallelism_threads = 1,  # config parallelism
                            # intra_op_parallelism_threads = 1,  # config parallelism
                            allow_soft_placement=True,
                            log_device_placement=True)
    with tf.Session(config=config) as sess:
        start_time = time.time()
        
        # 初始化所有变量
        init_op = tf.global_variables_initializer().run()
        
        print('Training and evaluating...')
        # 准备验证数据集，一般用于在训练过程中大致判断停止以及模型训练效果:
        validation_feed = {x: mnist.validation.images, y_: mnist.validation.labels}
        # 准备测试数据集，用于评价模型优劣的标准
        test_feed = {x: mnist.test.images, y_: mnist.test.labels}
        
        # 可视化准备
        epoch = 0
        NUM_EPOCH = int(TRAINING_STEPS / 1000)
        fig_loss = np.zeros([NUM_EPOCH])
        fig_acc_val = np.zeros([NUM_EPOCH])
        fig_acc_test = np.zeros([NUM_EPOCH])

        # 迭代训练神经网络
        for step in range(TRAINING_STEPS):
            
            # 产生这一轮使用的一个 batch 的训练数据，并进行训练
            xs, ys = mnist.train.next_batch(BATCH_SIZE)
            sess.run(train_op, feed_dict={x: xs, y_: ys})
            
            # 每 1000 次输出一次在验证数据上的测试结果
            if step % 1000 == 0:
                # print('Epoch:', epoch + 1)
                
                loss_train, acc_train = sess.run([loss, accuracy], feed_dict={x: xs, y_: ys})
                loss_val, acc_val = sess.run([loss, accuracy], feed_dict=validation_feed)  # todo
                time_dif = get_time_dif(start_time)
                msg = 'Iter: {0:>6}, Train Loss: {1:>6.2}, Train Acc: {2:>7.2%},' \
                        + ' Val Loss: {3:>6.2}, Val Acc: {4:>7.2%}, Time: {5}'
                print(msg.format(step, loss_train, acc_train, loss_val, acc_val, time_dif))
                
                # 可视化准备
                acc_test = sess.run(accuracy, feed_dict=test_feed)
                fig_loss[epoch] = loss_train
                fig_acc_val[epoch] = acc_val + 0.05  # 为了区分验证准确率和测试准确率差别, 让验证集准确率上移 0.05 单位
                fig_acc_test[epoch] = acc_test
                epoch += 1  
                
        # 训练结束后，在测试数据集上计算 FCNN 模型的最终准确率，以评估模型效果
        test_acc = sess.run(accuracy, feed_dict=test_feed)
        print ("After %d training step(s), test accuracy "
               "using average Model is %g " % (TRAINING_STEPS, test_acc))
        
        ### -------- 可视化 -------- ###
        # 训练过程中损失 (Loss) 曲线:
        fig1 = plt.figure()
        plt.plot(np.arange(NUM_EPOCH), fig_loss, label="Loss")
        plt.xlabel("Iteration")
        plt.ylabel("Training Loss")
        # plt.show()

        # 验证集和测试集上的准确率 (Accuracy) 曲线:
        # fig2 = plt.figure(figsize=(30, 1), dpi=50)  # 设置图片大小和像素(dpi=50)
        fig2 = plt.figure()
        plt.plot(np.arange(NUM_EPOCH), fig_acc_val, label="Validation Accuracy", color="blue")  # 绘制折线图
        plt.plot(np.arange(NUM_EPOCH), fig_acc_test, label="Test Accuracy", color="green")  # 绘制折线图
        plt.xlabel("Iteration")  # 设置 x 轴标签
        plt.ylabel("Modul Accuracy")  # 设置 y 轴标签
        y_ticks = np.arange(0, 1, 0.15)  # 设置 y 轴刻度
        plt.yticks(y_ticks) 
        plt.grid(alpha=0.4, linestyle='-.')  # 绘制网格 >>>> alpha 设置网格透明度; linestyle 设置网格样式
        # plt.legend(prop=my_font, loc='upper left')  # 设置图例字体及其位置 (默认右上)
        plt.show()
        ### ======================= ###


############################   Main Function as the begin of program  ###########################

def main(arg=None):

    ###################### Functions for downloading and reading MNIST data. ######################
    ''' 
    ## 初始化：下载或读取用于训练、测试以及验证的 MNIST 手写数字图片（28px * 28px）数据集 ##

        MNIST 数据集分成两部分：60000行的训练数据集（mnist.train）和10000行的测试数据集（mnist.test）。每一个 MNIST 数据单
    元（数据对象）有两部分组成：一张包含手写数字的图片和一个对应的标签。比如训练数据集的图片是 mnist.train.images ，训练数据集的标签是 mnist.train.labels。

        mnist.train.images 是一个形状为 [60000, 784] 的张量，第一个维度数字用来索引图片，第二个维度数字用来索引每张图片中的像素点。
        mnist.train.labels 是一个形状为 [60000, 10] 的张量，第一个维度数字用来索引图片，第二个维度数字用来索引每张图片中的分类标签（one-hot vectors）。

        实际，read_data_sets 类会将数据从原始数据包格式解析成训练和测试神经网络时的数据格式 。read_data_sets 会自动将 MNIST 数据集划分为 train（55000）、test（10000） 以及 validation（5000）三个数据集。
    '''
    print("Loading training and validation data...")
    start_time = time.time()
    
    # 指定 MNIST 数据集的下载和读取的路径：
    MNIST_DATA_PATH = "./MNIST_data/"
    mnist = input_data.read_data_sets(MNIST_DATA_PATH, one_hot=True)
    
    # print mnist.train dataSet size :
    print("Training Data Size : ", mnist.train.num_examples)
    # print mnist.validation dataSet size :
    print("Validation Data Size : ", mnist.validation.num_examples)
    # print mnist.test dataSet size :
    print("Testing Data Size : ", mnist.test.num_examples)
    
    # print mnist.train.images[0] / mnist.train.labels[0] Format
    # print("Example training data[0] pix-matirx : ", "\n", mnist.train.images[0])
    # print("Example training picture shape : " + str(len(mnist.train.images[0])))
    # print("Example training data lable : ", mnist.train.labels[0])
    # print("Example training lable shape : " + str(len(mnist.train.labels[0])))
    
    time_diff = get_time_dif(start_time)
    print("Time Usage:", time_diff)
    
    ###################### Functions for Training FCNN Model By Using MNIST data. ######################
    
    # begin to train model:
    train(mnist)


if __name__ == "__main__":
    # TF 提供的一个主程序入口，tf.app.run 会调用上面定义的 main 函数：
    # tf.app.run()
    main()

样例程序输出信息如下：

Loading training and validation data...
Extracting ./MNIST_data/train-images-idx3-ubyte.gz
Extracting ./MNIST_data/train-labels-idx1-ubyte.gz
Extracting ./MNIST_data/t10k-images-idx3-ubyte.gz
Extracting ./MNIST_data/t10k-labels-idx1-ubyte.gz
Training Data Size :  55000
Validation Data Size :  5000
Testing Data Size :  10000
Time Usage: 0:00:00.347534
Training and evaluating...
Iter:      0, Train Loss:    3.7, Train Acc:  57.00%, Val Loss:    4.5, Val Acc:  38.60%, Time: 0:00:00.421596
Iter:   1000, Train Loss:  0.094, Train Acc: 100.00%, Val Loss:   0.17, Val Acc:  97.18%, Time: 0:00:01.537846
Iter:   2000, Train Loss:  0.089, Train Acc: 100.00%, Val Loss:   0.15, Val Acc:  97.72%, Time: 0:00:02.682101
Iter:   3000, Train Loss:  0.083, Train Acc: 100.00%, Val Loss:   0.14, Val Acc:  97.96%, Time: 0:00:03.847363
Iter:   4000, Train Loss:  0.077, Train Acc: 100.00%, Val Loss:   0.14, Val Acc:  97.90%, Time: 0:00:05.014624
Iter:   5000, Train Loss:  0.068, Train Acc: 100.00%, Val Loss:   0.13, Val Acc:  98.08%, Time: 0:00:06.187306
Iter:   6000, Train Loss:  0.066, Train Acc: 100.00%, Val Loss:   0.12, Val Acc:  98.24%, Time: 0:00:07.310558
Iter:   7000, Train Loss:  0.065, Train Acc: 100.00%, Val Loss:   0.12, Val Acc:  98.20%, Time: 0:00:08.489824
Iter:   8000, Train Loss:  0.058, Train Acc: 100.00%, Val Loss:   0.11, Val Acc:  98.40%, Time: 0:00:09.660084
Iter:   9000, Train Loss:  0.059, Train Acc: 100.00%, Val Loss:   0.11, Val Acc:  98.42%, Time: 0:00:10.893361
Iter:  10000, Train Loss:  0.056, Train Acc: 100.00%, Val Loss:   0.11, Val Acc:  98.40%, Time: 0:00:12.093628
Iter:  11000, Train Loss:  0.053, Train Acc: 100.00%, Val Loss:   0.11, Val Acc:  98.42%, Time: 0:00:13.272892
Iter:  12000, Train Loss:  0.051, Train Acc: 100.00%, Val Loss:    0.1, Val Acc:  98.38%, Time: 0:00:14.393144
Iter:  13000, Train Loss:  0.051, Train Acc: 100.00%, Val Loss:    0.1, Val Acc:  98.40%, Time: 0:00:15.549404
Iter:  14000, Train Loss:  0.051, Train Acc: 100.00%, Val Loss:    0.1, Val Acc:  98.54%, Time: 0:00:16.730667
Iter:  15000, Train Loss:  0.045, Train Acc: 100.00%, Val Loss:  0.099, Val Acc:  98.48%, Time: 0:00:17.896928
Iter:  16000, Train Loss:  0.047, Train Acc: 100.00%, Val Loss:  0.099, Val Acc:  98.48%, Time: 0:00:19.068191
Iter:  17000, Train Loss:  0.044, Train Acc: 100.00%, Val Loss:  0.096, Val Acc:  98.50%, Time: 0:00:20.166436
Iter:  18000, Train Loss:  0.046, Train Acc: 100.00%, Val Loss:  0.096, Val Acc:  98.60%, Time: 0:00:21.333697
Iter:  19000, Train Loss:  0.044, Train Acc: 100.00%, Val Loss:  0.094, Val Acc:  98.56%, Time: 0:00:22.496959
Iter:  20000, Train Loss:  0.049, Train Acc: 100.00%, Val Loss:  0.094, Val Acc:  98.54%, Time: 0:00:23.666221
Iter:  21000, Train Loss:  0.044, Train Acc: 100.00%, Val Loss:  0.093, Val Acc:  98.52%, Time: 0:00:24.835482
Iter:  22000, Train Loss:  0.048, Train Acc: 100.00%, Val Loss:  0.093, Val Acc:  98.52%, Time: 0:00:26.002744
Iter:  23000, Train Loss:  0.041, Train Acc: 100.00%, Val Loss:  0.093, Val Acc:  98.46%, Time: 0:00:27.125994
Iter:  24000, Train Loss:  0.042, Train Acc: 100.00%, Val Loss:  0.092, Val Acc:  98.52%, Time: 0:00:28.296257
Iter:  25000, Train Loss:  0.047, Train Acc: 100.00%, Val Loss:  0.092, Val Acc:  98.54%, Time: 0:00:29.459517
Iter:  26000, Train Loss:   0.04, Train Acc: 100.00%, Val Loss:  0.091, Val Acc:  98.54%, Time: 0:00:30.612776
Iter:  27000, Train Loss:  0.043, Train Acc: 100.00%, Val Loss:  0.091, Val Acc:  98.58%, Time: 0:00:31.786038
Iter:  28000, Train Loss:  0.041, Train Acc: 100.00%, Val Loss:  0.091, Val Acc:  98.54%, Time: 0:00:32.886282
Iter:  29000, Train Loss:  0.041, Train Acc: 100.00%, Val Loss:   0.09, Val Acc:  98.54%, Time: 0:00:34.055544
After 30000 training step(s), test accuracy using average Model is 0.9828

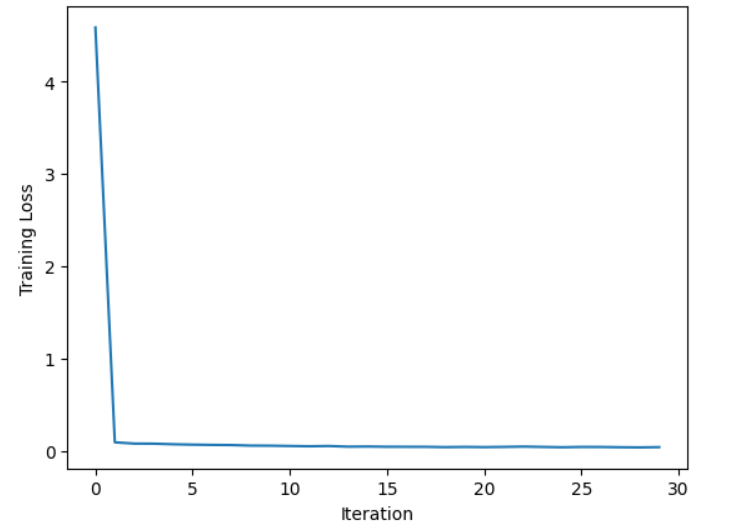
训练过程中损失 (Loss) 曲线如下：

可见，随着训练迭代过程的增加，模型的损失函数逐渐收敛于一个较小值（接近 0）。

训练过程中，验证集和测试集上的准确率 (Accuracy) 变化曲线:

可见，对于分布均匀的数据集，训练过程中模型在验证集上表现可以完全表征其在测试集上的效果！！！

---

模型效果评估

上述 TF 实现 MNIST 图像识别问题样例中，我们设置了一系列的参数：初始学习率、学习率衰减率、隐藏层节点数、迭代轮数等，并且我们知道神经网络模型的最终表达效果是受上述参数影响的。

那么如何设置这些参数的取值？！！大部分情况下，配置神经网络的参数是需要通过不断对比实验来进行调整，以实现最佳的神经网络模型效果（关于更多神经网络调参内容可参考【>>>> 一文详解深度神经网络调参技巧 <<<<】）。

那么，如何评估不同参数设置下的模型效果优劣？！！

---

测试集评估

神经网络模型效果的好坏可以通过 >>>> 模型对未知数据（测试集数据）的预测情况来评判的。

但我们不能直接通过模型在测试数据上的效果来选择参数（测试数据集变成了训练数据集的一部分参与训练，这时设置测试集是没有意义的；或者测试集较好表现成为模型优化的目标），这可能导致神经网络过度拟合测试数据，从而失去了对未知数据的预判能力。

也就是说，测试数据不应该对我们最终学得（/训练得到）的神经网络模型提供任何支持，这样才能 保证通过测试数据评估出来的模型效果和在真实场景下模型对未知数据的预测效果是最接近的！！！ <<<< 测试数据集对应的是部分未知数据，所以需要保证训练过程中测试数据不可见。

| ================================================== Split Line =============================================== |

由于测试数据在训练过程的不可见，那么如何评判在 优化/训练过程中 神经网络模型不同参数设置下的效果？！！

👇👇👇 引入验证集（Validation Set） 👇👇👇

一般会从训练集抽取一部分数据作为验证数据集，通过训练模型在验证数据集上的表现，来（代替测试集）评价优化过程中不同参数选取下模型的好坏。

👇👇👇 K 折（K Fold Cross Validation） 👇👇👇

一般是将整个数据集分成 k 个子集，每个子集均做一次测试集，其余的作为训练集进行训练。交叉验证需要重复 k 次，每次选择一个子集作为测试集，并将 k 次的平均交叉验证识别正确率作为结果。

由于神经网络本身训练时间就比较长，采用交叉验证会花费大量的时间（适合小数据集）。所以在海量数据下，一般会更多的采用验证数据集的形式来评测模型的效果。

---

验证集近似评估

为了说明 >>>> 验证数据可以代替测试集（默认数据分布均匀），近似作为模型效果的评价标准，我们将对比不同迭代轮数情况下，模型在验证数据和测试数据上的准确率：

上图给出了每 1000 轮 FCNN 模型在验证、测试数据集上的准确率变换曲线。可以看出，虽然两条曲线不完全重合，但这两条曲线的趋势基本一致，而且他们的相关系数（correlation coefficient）大于 0.9999。

实验说明 >>>> 模型在验证数据集上的表现，完全可以近似作为评价不同神经网络模型的标准，或者作为训练迭代轮数的依据！！！

| ================================================== Split Line =============================================== |

👇👇👇 需要注意的是 👇👇👇

上面我们所说的测试数据集训练过程不可见，并不是严格不可见。你会看到很多资料不会划分验证数据集，直接使用测试数据集作为模型训练过程中是否近优的评价标准。

个人理解 >>>> 理想情况下，我们希望选取的未划分的样本数据集样本对于问题的数据分布是均匀的。但如果验证数据分布不能很好地代表测试数据分布，那么模型在这两个数据集上的表现就可能不一样。

一般来说，选取的验证数据分布越接近测试数据分布，模型在验证数据上的表现就越可以体现神经网络模型在测试数据（未知数据）下的效果！！！

---

不同优化方法模型效果对比

了解了神经网络模型效果评估标准后，这一小节将通过模型在 MNIST 测试集上的预测准确率表现对比上一篇博文中提到的神经网络结构设计和参数优化的不同方法，从实际问题中展示不同优化方法所带来的性能提升。

下图，给出了在相同神经网络参数下，设置不同优化方法的对比实验，经过 30000 轮训练迭代后，得到的各个模型最终的正确率（10 次运行结果的平均值）：

👇👇👇 神经网路模型结构影响 👇👇👇

可以看出 >>>> 调整神经网络模型的结构（不使用隐藏层或没有激活函数）对最终的准确率有非常大的影响。这说明神经网络的结构设计对最终模型的效果有本质的影响。

后面会介绍一种更加特殊的神经网络结构 CNN（卷积神经网络），它可以更加有效的处理图像信息。通过 CNN 可以进一步将 MNIST 识别模型准确率提高到 99.5%。

👇👇👇 滑动平均模型/指数衰减学习率/正则化影响 👇👇👇

从上图数字中发现 >>>> 使用滑动平均模型、指数衰减学习率和使用正则化带来的正确率提升并不是特别明显。其中，使用了所有优化方法的模型、和不使用滑动平均模型，以及不使用指数衰减学习率的模型正确率都可以达到约 98.4% 。

那么是不是意味着这些优化方法对模型准确率提升不大？！！

答案肯定是否定的！！！这里准确率提升不是特别明显，是由于 MNIST 数据集简单，模型收敛速度很快（梯度较小），而滑动平均模型以及指数衰减学习率在一定程度上都是限制神经网络中参数的更新速度，所以这两种优化对最终模型影响不大。

从上面模型在验证数据和测试数据上的准确率曲线可以看出，在迭代 4000 次以后就已经接近最终的准确率了（收敛太快）。

| ================================================== Split Line =============================================== |

下面我们将进一步分析滑动平均模型、指数衰减学习率和使用正则化对训练模型的影响：

[1] >>>> 滑动平均模型和指数衰减学习率

先给出不同迭代轮数时，使用了所有优化方法的模型的正确率与平均绝对梯度的变化趋势图：

可以看出，前 4000 轮迭代对模型的改变是最大的。在 4000 轮迭代之后，由于梯度比较小，所以参数的改变也就比较缓慢了。于是滑动平均模型或者指数衰减学习率的作用也就没那么显著了。

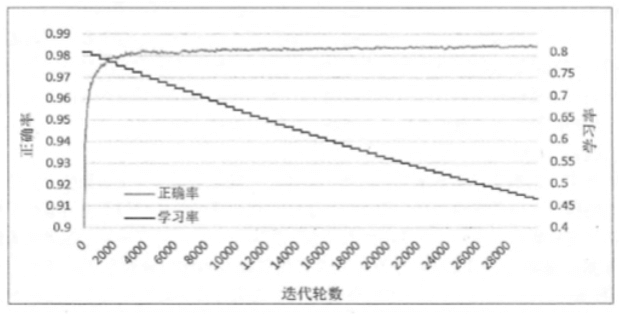
不同迭代轮数时，模型正确率和衰减之后学习率的变化趋势图如下：

可以看出，学习率曲线呈现阶梯状衰减方式。在前 4000 轮时，衰减之后的学习率和初始学习率的差距并不大。那么，能否说明这些限制网络参数的更新速度的优化方法作用不大？！！

实际上，当问题更加复杂时，模型迭代不会这么快收敛，这时滑动平均模型和指数衰减学习率会发挥更大的作用！！！例如 Cifar-10 图像分类数据集上，使用滑动平均模型可以将模型识别的错误率降低 11%，使用指数衰减学习率可以将识别错误率降低 7%。

| ================================================== Split Line =============================================== |

[2] >>>> 正则化

相较于滑动平均模型和指数衰减学习率，使用加入了正则化损失函数（结构风险）给模型效果带来的提升要相对显著。

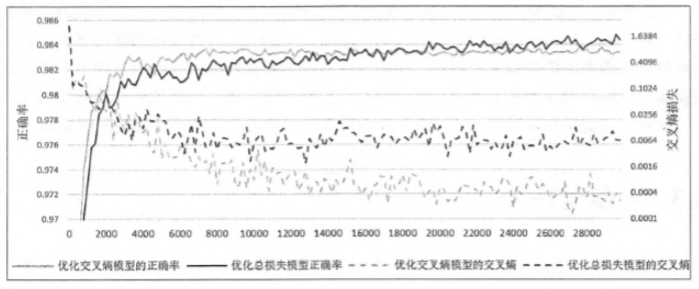
下图对比了两个使用了不同损失函数的神经网络模型，其中一个模型只最小化交叉熵损失，另一个模型优化的是交叉熵损失和 L2 正则化损失的和：

显而易见，只优化交叉熵的模型在训练数据上的交叉熵损失（灰色虚线）要比优化总损失的模型更小（黑色虚线）。然而在测试数据上，优化总损失的模型（黑色实线）却要好于只优化交叉熵的模型（灰色实线）。这就是前面我们提到过的过拟合问题。

这是由于只优化交叉熵的模型可能更好的拟合训练数据（损失更小），却不能很好的挖掘数据中的潜在规律来判断未知的测试数据，故在测试数据上的准确率低。

我们再给出不同模型的损失函数变化规律：

从左侧只优化交叉熵模型子图可以看出，随着迭代的进行，正则化损失是在不断增大的。

而由于 MNIST 问题相对比较简单，迭代后期的梯度很小，所以正则化损失的增长也很慢。对于更加复杂的问题，迭代后期的梯度更大，就会发现总损失（交叉熵损失加上正则化损失）会呈现一个 U 型！！！

| ================================================== Split Line =============================================== |

↓↓↓↓↓↓ 结论 ↓↓↓↓↓↓

可以发现，上述的这些优化方法确实可以解决前面博文中提到的神经网络优化过程中的问题。当需要解决的问题和使用到的神经网络模型更加复杂时，上面的这些优化方法将更有可能对训练效果产生更大的影响。

---

TF 变量命名空间管理

由于编程习惯，我们通常喜欢采用模块化编程风格，提高代码可读性。

上面给出的 TF 实现 MNIST 手写体数字图像识别示例中，将计算神经网络前向传播结果的过程抽象成了一个函数（模块）:

def inference(input_tensor, avg_class, weights1, biases1, weights2, biases2)

这样带来的一个好处：在训练、测试以及预测的过程中可以统一调用同一个函数来得到模型的前向传播结果。

---

变量的重用以及命名空间

从上述 FP 过程定义中可以看到，这个函数的形参中需要包括神经网络中的所有参数。

你想过没有：当神经网络的结构更加复杂，引入的参数更多时，就需要一个更好的方式来传递和管理神经网络中的参数了 >>>> TensorFlow 支持通过变量名称来创建或者获取一个变量的机制。

通过这种机制，我们可以在不同函数中可以直接通过变量的名称来使用变量（变量重用），而不要将变量通过参数的形式到处传递。

TF 中通过 tf.get_variable 函数和 tf.variable_scope 函数来分别实现 TF 变量的重用和命名空间管理。

---

TF 变量重用

除了之前提到过的 tf.Variable() 变量创建函数，TensorFlow 中还支持通过 tf.get_variable 函数来获取已存在变量（不存在则创建）。

[1] >>>> tf.Variable

重新认识一下 tf.Variable() 函数：

tf.Variable 函数用于生成一个初始值为 initial-value 的变量（必须指定初始化值）：

tf.Variable(
    initial_value=None, 
    trainable=True, 
    collections=None, 
    validate_shape=True, 
    caching_device=None, 
    name=None, 
    variable_def=None, 
    dtype=None, 
    expected_shape=None, 
    import_scope=None
)

经常使用的是：initial_value（初始化）、name（命名）、dtype（变量类型）、trainable（是否可训练/优化）。

↓↓↓↓↓↓ 参数解释 ↓↓↓↓↓↓

• initial_value：Variable 初始值，为 Tensor 或可转换为 Tensor 的 Python 对象。如果 validate_shape = True（默认），则初始值必须具有指定的形状；
• validate_shape：默认为 True，initial_value 必须具有指定的形状。如果为 False，则允许使用未知形状的值初始化变量；
• name：变量的可选名称，默认为 “Variable” 并自动获取；
• dtype：如果设置，则 initial_value 将转换为给定类型；如果为 None，则保留数据类型；
• trainable：用于标识模型训练时是否更新当前参数；如果为 True，当前变量会被添加到图形集合 GraphKeys.TRAINABLE_VARIABLES中；
• collections：